Az állítás nyilván nem igaz az üres gráfra; ezért továbbiakban feltételezzük, hogy a gráfnak van legalább egy csúcsa. Mivel ennek a csúcsnak legalább 3 szomszédja van, a csúcsok száma legalább 4.

Először bebizonyítjuk, hogy ha egy nem üres gráfban minden csúcs foka legalább 2, akkor a gráf tartalmaz kört. Képezzük csúcsok egy $A_0$, $A_1$, $\text{...}$ sorozatát a következőképpen. Legyen $A_0$ és $A_1$ két szomszédos csúcs. Ha valamely $n\ge 1$-re $A_n$-et már definiáltuk, akkor legyen $A_{n+1}$ az $A_n$-nek az egyik, $A_{n-1}$-től különböző szomszédja. Ilyen mindig létezik, mert $A_n$-nek a feltétel szerint legalább két szomszédja van. Mivel a gráfnak csak véges sok csúcsa van, bizonyos csúcsok a sorozatban többször szerepelnek. Legyen $A_m$ az első olyan eleme a sorozatnak, ami korábban már szerepelt: $A_m=A_k$ valamely $k<m$-re. Ekkor nyilván $m>k+2$ (a gráf egyszerű), és így az $A_k$, $A_{k+1}$, $\text{...}$, $A_{m-1}$ csúcsok egy kört alkotnak.
Válasszuk ki most a gráf egy tetszőleges $C$ csúcsát. A gráf tartalmaz olyan kört, amely nem megy át $C$-n. Ha ugyanis a $C$ csúcsot a belőle induló élekkel együtt elhagyjuk, a megmaradó gráf legalább 3 csúcsot tartalmaz, és mindegyik csúcs foka legalább 2; az előbbiek szerint ez a gráf tartalmaz kört.
Ha egy $C$-n át nem menő kör éleit elhagyjuk, a gráf esetleg több komponensre esik szét. Legyen $K$ az egyik $C$-n át nem menő kör, amelyre a $C$-t tartalmazó komponens maximális számú csúcsot tartalmaz. Megmutatjuk, hogy $K$ éleit elhagyva a gráf összefüggő marad.
Tegyük fel, hogy $K$ éleit elhagyva a gráf legalább két komponensre esik szét. Az eredeti gráfbeli utakkal bármelyik két komponens pontjai összeköthetők. A $K$ éleinek elhagyása után ezekből az utakból csupán $K$ élei hiányozhatnak; ebből látható, hogy minden komponensnek van közös csúcsa a $K$ körrel.
Legyen $G_1$ az a komponens, amely $C$-t tartalmazza, $G_2$ pedig egy ettől különböző komponens. Mindkét komponensnek van legalább egy közös csúcsa a $K$ körrel; legyen egy-egy ilyen csúcs $D$, illetve $E$. Két esetet fogunk vizsgálni aszerint, hogy $G_2$-nek és $K$-nak van-e $E$-kívül más közös csúcsa.
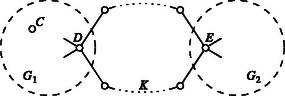
Vizsgáljuk először azt az esetet, amikor $G_2$-nek és $K$-nak az $E$ az egyetlen közös csúcsa (1. ábra). Mivel $E$-nek legalább három szomszédja van, és ezek közül csak kettő tartozik a $K$ körhöz, legalább egy szomszédja $G_2$-ben van; a $G_2$ komponens tehát legalább még egy csúcsot tartalmaz. Tekintsük most azt a gráfot, amelyet úgy kapunk, hogy $G_2$-ből elhagyjuk $E$-t és a belőle induló éleket. Ez a gráf nem üres, és minden csúcsa legalább másodfokú. A gráf tehát tartalmaz egy $K\text{'}$ kört. Ha eredetileg a $K$ kör helyett ennek a $K\text{'}$ körnek az éleit hagytuk volna el, akkor a $C$-t tartalmazó komponensnek része lenne a $G_1$ gráf és az $E$ csúcs is; ez ellentmond annak, hogy a $G_1$ komponens éleinek száma maximális.
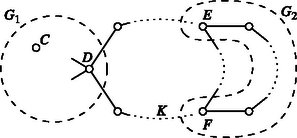
Most vizsgáljuk azt az esetet, amikor $G_2$-nek és $K$-nak $E$-n kívül még legalább egy közös csúcsa van; legyen egy ilyen csúcs $F$. Feltételezzük, hogy a $K$ körnek a $D$-t nem tartalmazó $EF$ ívén a $G_2$ komponensnek nincs több csúcsa; ezt mindig elérhetjük úgy, hogy az $E$ és $F$ csúcsot a $K$ és $G_2$ más, megfelelő közös csúcsaira cseréljük (2. ábra).
Mivel a $G_2$ komponens összefüggő, az $E$ és $F$ pontok összeköthetők $G_2$-beli élekkel. Ez az út a $K$ körnek a $D$-t nem tartalmazó $EF$ szakaszával együtt egy $K\text{'}$ kört alkot. Ha a $K$ helyett a $K\text{'}$ kör éleit hagytuk volna el, akkor a $C$-t tartalmazó komponens ismét tartalmazná $G_1$ valamennyi pontját, és $K$ megmaradó élei révén tartalmazná a $DE$ és a $DF$ íveknek legalább egy-egy további pontját is. Ez ismét ellentmond annak, hogy $G_1$ maximális.

Tehát a $K$ kör éleinek elhagyása után a gráf valóban összefüggő marad.