Kezdőlap


Feladat:	C.584	Korcsoport: 18-	Nehézségi fok: könnyű
Megoldó(k):	Erdei Zsuzsa
Füzet:	2001/január, 25 - 26. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai számítások trigonometriával, Körök, Szabályos sokszögek geometriája, Terület, felszín, C gyakorlat
Hivatkozás(ok):	Feladatok: 2000/április: C.584

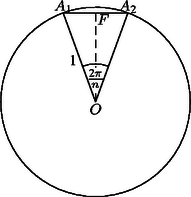
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az általánosság megszorítása nélkül feltehetjük, hogy a kör sugara egységnyi. Legyen a kör középpontja $O$ , a szabályos $n$ -szög egyik oldala $A_{1} A_{2}$ , a hozzá tartozó középponti szög $\frac{2 π}{n}$ , az $A_{1} A_{2}$ szakasz felezőpontja $F$ .
Az $A_{1} O A_{2}$ háromszög területe $\frac{1 \cdot 1 \cdot sin \frac{2 π}{n}}{2}$ , így a sokszög területe

\begin{matrix} T = \frac{n}{2} sin \frac{2 π}{n} . \end{matrix}

Legyen

A_{1} A_{2} = 2 x

, ahol

x = sin \frac{π}{n}

O A_{1} F

derékszögű háromszögből. A sokszög kerülete:

\begin{matrix} K = n 2 x = 2 n sin \frac{π}{n} . \end{matrix}

A pontos érték és a közelítő érték különbségének arányát a pontos értékhez relatív hibának nevezzük.
Írjuk fel a terület és a kerület relatív hibáját.

\begin{matrix} \begin{matrix} T_{h} & = \frac{π - \frac{n}{2} sin \frac{2 π}{n}}{π} = 1 - \frac{n sin \frac{2 π}{n}}{2 π}, \\ K_{h} & = \frac{2 π - 2 n sin \frac{π}{n}}{2 π} = 1 - \frac{2 n sin \frac{π}{n}}{2 π} . \end{matrix} \end{matrix}

Képezzük a terület és kerület relatív hibájának különbségét.

\begin{matrix} T_{h} - K_{h} = \frac{2 n sin \frac{π}{n}}{2 π} - \frac{n sin \frac{2 π}{n}}{2 π} = \frac{n}{π} (2 sin \frac{π}{n} - sin \frac{2 π}{n}) . \end{matrix}

\frac{n}{2 π} > 0

, és

0 < \frac{π}{n} < \frac{π}{2}

, mivel

n

legalább 3.
Felhasználjuk a

sin 2 α = 2 sin α cos α

összefüggést, ekkor a zárójelben lévő különbség:

\begin{matrix} 2 sin \frac{π}{n} - sin \frac{2 π}{n} = 2 sin \frac{π}{n} - 2 sin \frac{π}{n} cos \frac{π}{n} = 2 sin \frac{π}{n} (1 - cos \frac{π}{n}) . \end{matrix}

0 < \frac{π}{n} < \frac{π}{2}

összefüggés miatt

sin \frac{π}{n} > 0

és

cos \frac{π}{n} < 1

, azaz

1 - cos \frac{π}{n} > 0

.
A relatív hibák különbsége pozitív, vagyis a körbe írt szabályos sokszöggel számolva a kör kerületét kisebb relatív hibával tudjuk közelíteni, mint a területet.

Erdei Zsuzsa (Hajdúszoboszló, Hőgyes E. Gimn., 10. o.t.)