Kezdőlap


Feladat:	1738. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Balogh László , Fodor Zoltán , Ván Péter
Füzet:	1982/március, 139 - 140. oldal		PDF \| MathML
Témakör(ök):	Körmozgás (Tömegpont mozgásegyenlete), Rugalmas energia, Energia homogén gravitációs mezőben, Munkatétel, Egyéb körmozgás, Feladat
Hivatkozás(ok):	Feladatok: 1981/november: 1738. fizika feladat

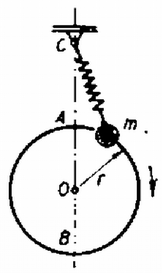
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás.

a) Ha az

m

tömegű test éppen a

B

pontig jut el, ez azt jelenti, hogy sebessége és így mozgási energiája az

A

és

B

pontokban egyaránt nulla, tehát a helyzeti energia és a rugó rugalmas energiájának összege a két pontban azonos:

\begin{matrix} (1 / 2) D x_{0}^{2} + m g \cdot 2 r = (1 / 2) D {(x_{0} + 2 r)}^{2}, \end{matrix}

(1)

ahol

x_{0} = (k - 1) r - L

. Innen a szükséges tömeg:

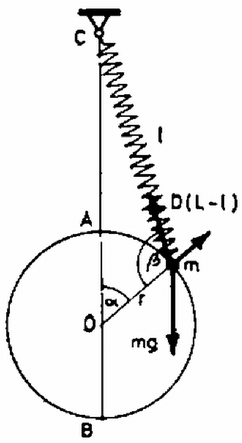
\begin{matrix} m = (D / g) (k r - L) = 4, 8 kg. \end{matrix}

(2)

b) A legnagyobb sebességet a test az egyensúlyi helyzeten való áthaladáskor veszi föl.

A testre az

m g

súlyerő, a rugóerő és egy sugárirányú kényszererő hat. Így a tömeg akkor lesz nyugalomban, ha a súlyerő és a rugóerő érintő irányú összetevője egyenlő:

\begin{matrix} D (l - L) cos (β - 90^{\circ}) = m g sin α . \end{matrix}

(3)

Itt

l

a rugó pillanatnyi hossza, a cosinustételből:

\begin{matrix} l = r \sqrt[]{k^{2} + 1 - 2 k cos α} = r y \end{matrix}

(4)

(bevezetve az

y

új változót, amit majd a II. megoldásban használunk fel). A rugó irányát jellemző

β

szög a sinustételből határozható meg

\begin{matrix} \frac{sin β}{sin α} = \frac{k r}{l} . \end{matrix}

(5)

A (3)‐(5) egyenletek felhasználásával a kifejezhető:

\begin{matrix} α = arc cos [\frac{k^{2} + 1}{2 k} - \frac{k L^{2} D^{2}}{2 {(k D r - m g)}^{2}}] . \end{matrix}

(6)

m

értékét (2)-ből behelyettesítve

\begin{matrix} α = arc cos [1 / (2 k)] \approx 75, 5^{\circ} . \end{matrix}

Balogh László (Budapest, Apáczai Csere J. Gyak. Gimn., II. o. t.)

II. megoldás. A feladat b) része annak alapján is megoldható, hogy abban a pontban, ahol a test sebessége és mozgási energiája maximális, a helyzeti- és rugóenergia összege minimális. Egy tetszőleges helyzetben

\begin{matrix} E_{h} + E_{r} = (1 / 2) D {(l - L)}^{2} + m g r cos α = \frac{1}{2} D {(r y - L)}^{2} + m g r \frac{k^{2} + 1 - y^{2}}{2 k}, \end{matrix}

(7)

ahol

l

-et és

cos α

-t (4)-bőI

y

-nal fejeztük ki. Az energia szélsőértékeit deriváltjának nulla-helyei adják. Közvetett függvényként deriválva

\begin{matrix} \frac{d}{d α} (E_{h} + E_{r}) = \frac{d}{d y} (E_{h} + E_{r}) \frac{d y}{d α} = (D r^{2} y - D r L - \frac{m g r}{k} y) \frac{k sin α}{\sqrt[]{k^{2} + 1 - 2 k cos α}} . \end{matrix}

(8)

sin α = 0

esetnek megfelelő

α_{1} = 0^{\circ}

és

α_{2} = 180^{\circ}

megoldások az

A

és

B

pontokat adják, ezekben a sebesség minimális. Ha a másik tényező nulla, az

\begin{matrix} y = \frac{D L k}{D r k - m g} \end{matrix}

(9)

eredményre jutunk. (2)-t beírva

y = k

α

-ra az előző megoldás eredménye adódik.

Fodor Zoltán (Budapest, Radnóti M. Gyak. Gimn., III. o. t.)

Megjegyzés. Diszkutáljuk eredményünket

m

függvényében a többi paramétert változatlatul hagyva!
Ha

m

nagyon nagy, a test nyilván körben mozog a pálya mentén, sebessége pedig

B

-ben a legnagyobb. Ez addig van így, amíg (9)-ből

y

-ra és onnan

α

-ra értelmes eredmény nem adódik, vagyis

α = 180^{\circ}

, (4)-ből

y = 3

nem lesz. (9)-ből ekkor

m = 5, 87

kg adódik. Ha

4, 8 kg<m<5,87

kg, a tömeg körben mozog, de sebessége már egy közbülső

α

helyzetben a legnagyobb. A tömeget tovább csökkentve az

m

tömegű test ide-oda mozog egészen addig, amíg a maximális sebességű helyet jellemző

α

szög

0^{\circ}

-ká nem válik. Ekkor

y = 1

m = 1, 6

kg. Ha

m < 1, 6

kg, az

A

pont stabil egyensúlyi helyzet, mozgás nem jön létre.