Kezdőlap


Feladat:	B.3328	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Hablicsek Márton
Füzet:	2000/november, 483. oldal		PDF \| MathML
Témakör(ök):	Érintősokszögek, Konvex sokszögek, Hossz, kerület, Eltolás, Feladat
Hivatkozás(ok):	Feladatok: 1999/december: B.3328

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen $A_{1} A_{2} ... A_{n}$ egy konvex $n$ -szög ( $n \geq 3$ ). Vizsgáljuk meg, mi történik az $A_{i}$ csúcsnál a transzformáció után. Legyenek $A_{i}$ merőleges vetületei az eltolt oldalegyeneseken $B_{i}$ és $D_{i}$ , az egyenesek metszéspontja pedig $C_{i}$ . Mivel $A_{i} B_{i}$ és $A_{i} D_{i}$ is 5 cm, azért $B_{i}$ és $D_{i}$ rajta van az $A_{i}$ körüli 5 cm sugarú körön, továbbá $C_{i} B_{i}$ és $C_{i} D_{i}$ a kör érintői, hiszen $A_{i} B_{i} C_{i}$ és $A_{i} D_{i} C_{i}$ derékszög.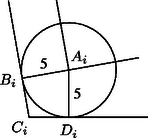

1. ábra

Vizsgáljuk a

B_{i} A_{i} D_{i}

szögek összegét. Ezek a konvex sokszög

A_{i}

-nél lévő belső szögeinek kiegészítő szögei (a két derékszög miatt). Így

\begin{matrix} \sum_{i = 1}^{n} B_{i} A_{i} D_{i} = n \cdot 180^{\circ} - (n - 2) \cdot 180^{\circ} = 360^{\circ} . \end{matrix}

Emiatt az

A_{i} B_{i} C_{i} D_{i}

négyszögeket az egyenlő hosszú, 5 cm-es oldalaiknál összeillesztve egy

n

oldalú érintősokszöget kapunk, amelynek beírt köre az 5 cm sugarú kör.
Állítjuk, hogy az érintősokszög

K

kerülete nagyobb a beírt kör kerületénél. Ez azért igaz, mert a sokszöget felbonthatjuk olyan háromszögekre, amelyek egyik oldala a sokszög oldala, ezzel szemközti csúcsa pedig a kör középpontja. Ezek közös magassága

r

, a kör sugara. A háromszögek területének összege tehát

\frac{K r}{2}

. Ez nagyobb, mint a kör területe, tehát

r^{2} π < \frac{K r}{2}

. Ebből pedig valóban

2 r π < K

. A feladatban

r = 5

cm. Ezt behelyettesítve:

2 \cdot 5 \cdot π < K

, ahonnan

30 < K

következik.
Vegyük még észre, hogy az érintősokszög kerülete éppen annyi, amennyivel az eredeti sokszög kerülete nőtt a transzformáció után, és így a növekedés értéke valóban több, mint 30 cm.

Hablicsek Márton (Fazekas M. Főv. Gyak. Gimn., 8. o.t.)

Megjegyzés. A fenti megoldás szemléltethető a következőképpen (2., 3. ábra):

2. ábra

3. ábra