Feladat:	B.3323	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Gáspár Merse Előd ,  Gerencsér Balázs ,  Hablicsek Márton ,  Kovács Erika Renáta
Füzet:	2000/május, 291 - 294. oldal		PDF  |  MathML
Témakör(ök):	Racionális számok és tulajdonságaik, Oszthatóság, Diofantikus egyenletek, Fagráfok, erdők, faváz, Feladat
Hivatkozás(ok):	Feladatok: 1999/december: B.3323

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. A feladatot megoldjuk, ha megkeressük I. azokat az $a$ és $b$ pozitív egész számokat, amelyekre $b<99$, $\frac{a}{b}<\frac{19}{99}$ és $\frac{a}{b}$ az ilyen törtek közül a legnagyobb; illetve II. azokat a $c$ és $d$ pozitív egész számokat, amelyekre $d<99$, $\frac{c}{d}>\frac{19}{99}$ és $\frac{c}{d}$ az ilyen törtek közül a legkisebb.   I. Vizsgáljuk a $D=\frac{19}{99}-\frac{a}{b}=\frac{19b-99a}{99b}>0$ különbséget! Legyen először $19b-99a=1$. Ekkor $19b=99a+1$, amiből $b=5a+\frac{4a+1}{19}$. Mivel $b<99$, azért $a$ kisebb, mint 20. Így a számláló, a $4a+1$ értéke 19 páratlan többszöröseként 19 vagy 57. A 19 nem megfelelő, mivel 18 nem osztható 4-gyel. Így $4a+1=57$, $a=14$ és $b=73$, a tört pedig $\frac{14}{73}$. Ebben az esetben $D=\frac{1}{99\cdot 73}$. Ez a legkisebb különbség, mivel ha $D$ számlálója egynél nagyobb lenne, akkor a nevezőben csak 99-nél nagyobb $b$ esetén lehetne a tört kevesebb, mint $\frac{1}{99\cdot 73}$. II. Vizsgáljuk most is a $D=\frac{c}{d}-\frac{19}{99}=\frac{99c-19d}{99d}>0$ különbséget! Legyen először $99c-19d=1$. Ekkor $19d=99c-1$, amiből $d=5c+\frac{4c-1}{19}$. Mivel $d<99$, azért $c$ kisebb, mint 20. Így a számláló, $4c-1$ értéke 19; 57 vagy 95. 57 nem megfelelő, mivel 18 nem osztható 4-gyel. 95 esetén $c=19$ és $d=100$, túl nagy. Így $4c-1=19$, $c=5$ és $d=26$. Ebben az esetben $D=\frac{1}{99\cdot 26}$. Ha ennél kisebb különbséget keresünk, akkor ha $D$ számlálója $e$, akkor $d$ legalább $26e<99$. Emiatt a $D$ számlálója legfeljebb 3. Ha $99c-19d=2$, akkor $19d=99c-2$, amiből $d=5c+\frac{4c-2}{19}$. A fentiekhez hasonlóan ellenőrizhető, hogy csak a $4c-2=38$ a megoldás, amiből $c=10$ és $d=52$. Ha $99c-19d=3$, akkor $19d=99c-3$, amiből $d=5c+\frac{4c-3}{19}$. Most csak a $4c-3=57$ a megoldás, amiből $c=15$ és $d=78$. Mindhárom eredmény az $\frac{5}{26}$ törtet adja. A feladat megoldása tehát: $\frac{14}{73}<x<\frac{5}{26}$ az a legbővebb (nyílt) intervallum, ahol a $\frac{19}{99}$ a legkisebb nevezőjű tört.  Hablicsek Márton (Fazekas M. Főv. Gyak. Gimn., 8. o.t.)   II. megoldás. Megmutatjuk, hogy ha $0<\frac{a}{b}<\frac{19}{99}$ és $19b-99a=1$, akkor az $\left(\frac{a}{b};\frac{19}{99}\right)$ intervallumban minden tört nevezője nagyobb 99-nél ‐ valójában, mint látni fogjuk majd, $99+b$-nél is. Legyen tehát $0<\frac{a}{b}<\frac{p}{q}<\frac{19}{99}$. A nevezőkkel szorozva $99aq<bp\cdot 99<19bq$. Így $q=19bq-99aq=19bq-99bp+99bp-99aq=\left(19q-99p\right)b+\left(bp-aq\right)\cdot 99\ge b+99$ (1. ábra).   1. ábra   Ugyanígy igazolható, hogy ha $\frac{19}{99}<\frac{c}{d}$ és $99c-19d=1$, akkor a $\left(\frac{19}{99};\frac{c}{d}\right)$ intervallumban minden tört nevezője nagyobb, mint $99+d$. A megoldáshoz tehát meg kell keresnünk azt a legkisebb pozitív $b$, illetve $d$ nevezőt, amelyre $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{ccc}\hfill {\displaystyle 19b-99a}& {\displaystyle =\mathrm{1,}\text{<span style="font-weight: normal;font-style: normal;">illetve</span>}}\hfill & \hfill {\displaystyle \left(1\right)}\\ \hfill {\displaystyle 99c-19d}& {\displaystyle =1.}\hfill & \hfill {\displaystyle \left(2\right)}\end{array}}}\end{array}$ Ismeretes, hogy ‐ mivel $\left(\mathrm{19,}99\right)=1$, a fenti egyenleteknek van, mégpedig pontosan egy olyan $\left(b\mathrm{,}a\right)$, illetve $\left(d\mathrm{,}c\right)$ megoldása, hogy $0<b<99$ és $0<a<19$, illetve $0<d<99$ és $0<c<19$, sőt, a $19b-99a=99c-19d$ egyenlőség átrendezésével kapott $19\left(d+b\right)=99\left(a+c\right)$ feltételből ezekre a minimális megoldásokra $d+b=99$ és $a+c=19$. Az (1), (2) ún. diofantikus egyenletek megoldására több módszer ismeretes ‐ az I. megoldásban valójában ezeket az egyenleteket oldotta meg a beküldő ‐ és ezek bármelyikével $b=73$, tehát $d=99-73=26$, $a=14$, tehát $c=19-14=5$, a maximális intervallum pedig, amelyben $\frac{19}{99}$ a minimális nevezőjű tört, $\left(\frac{14}{73}\mathrm{,}\frac{5}{26}\right)$.   Megjegyzések. 1. A megoldásból kiderül, hogy a keresett intervallumban $\frac{19}{99}=\frac{14+5}{73+26}$, a két végpont, $\frac{14}{73}$ és $\frac{5}{26}$ úgynevezett mediánja. A mediánképzés segítségével a $0=\frac{0}{1}$ és az $1=\frac{1}{1}$ törtekből kiindulva a $\left[\mathrm{0,}1\right]$ intervallum bármely törtjéhez eljuthatunk, ezeket redukált ‐ azaz egyszerűsített ‐ alakban kapjuk, és minden $\frac{p}{q}$ tört a legbővebb olyan intervallum két végpontjának a mediánjaként áll elő, amelyben $\frac{p}{q}$ a minimális nevezőjű tört. A konstrukció leírása megtalálható Graham‐Knuth‐Patashnik: Konkrét matematika (Műszaki Könyvkiadó, 1998) c. könyve 117‐119. oldalán. A fenti könyv 118. oldalán a konstrukciót megvalósító, ún. Stern‐Brocot-fa kezdete látható (2. ábra). 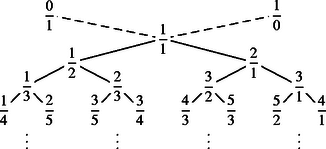  2. ábra   A fában az ,,$\frac{1}{0}$'' szimbólum segítségével az 1-nél nagyobb törteket is megkapjuk. Ha úgy tetszik ‐ mint ahogyan a margón olvasható ,,graffiti'' mondja, $\frac{1}{0}$ értelmezhető a ,,végtelennek nem redukálható tört alakjában történő előállításaként''. A fában minden tört az első balra, illetve jobbra felfelé útbaejtett szám mediánja. A Stern‐Brocot-fa felhasználásával oldotta meg a feladatot Gerencsér Balázs és Kovács Erika Renáta (mindketten a Fazekas M. Főv. Gyak. Gimn., 10. osztályos tanulói). A hivatkozás után a feladat annyi, hogy a $\frac{19}{99}$ törtet kell megtalálni a fában. A két tört, amelynek mediánjaként megtaláltuk, határolja a keresett intervallumot. Az alábbiakban Gerencsér Balázs ábrájának egy tipográfiailag módosított változatán mutatjuk be a $\frac{19}{99}$ felkutatását a fában. Induljunk el az egyik kezdőpontból, és mindig a $\frac{19}{99}$ felé lépjünk tovább: ha az éppen érintett szám nagyobb, mint $\frac{19}{99}$, akkor balra, ha pedig kisebb, akkor jobbra lépjünk a fában (3. ábra). 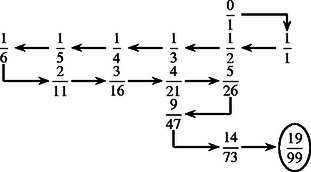  3. ábra   A $\frac{19}{99}$ a $\frac{14}{73}$ és az $\frac{5}{26}$ mediánjaként adódott, a keresett intervallum tehát $\left(\frac{14}{73}\mathrm{,}\frac{5}{26}\right)$. 2. A redukált törtek fenti származtatásával áll szoros kapcsolatban a 0 és 1 közé eső törtek Farey-sorozatokba történő elrendezése. Erről olvashatunk többek között ‐ a már idézett könyv 119‐120. oldalán, továbbá a KöMaL 1999/1. és 2. számában megjelent Holló-Szabó Ferenc: A Riemann-függvényről című cikkében. $N$-edrendű Farey-sorozatnak nevezzük és ${\text{F}}_N$-nel jelöljük a 0 és 1 közötti olyan redukált törtek növekvően rendezett sorozatát, amelyek nevezője nem nagyobb, mint $N$. Például $\begin{array}{c}{\displaystyle {\text{F}}_6=\frac{0}{1}\mathrm{,}\frac{1}{6}\mathrm{,}\frac{1}{5}\mathrm{,}\frac{1}{4}\mathrm{,}\frac{1}{3}\mathrm{,}\frac{2}{5}\mathrm{,}\frac{1}{2}\mathrm{,}\frac{3}{5}\mathrm{,}\frac{2}{3}\mathrm{,}\frac{3}{4}\mathrm{,}\frac{4}{5}\mathrm{,}\frac{5}{6}\mathrm{,}\frac{1}{1}\mathrm{.}}\end{array}$ ${\text{F}}_N$-et megkapjuk, ha ${\text{F}}_1=\frac{0}{1}\mathrm{,}\frac{1}{1}$-ből indulva mindannyiszor beszúrjuk a mediánokat, valahányszor a nevező nem nagyobb, mint $N$. ${\text{F}}_N$ bármely két szomszédos $\frac{a}{b}$, $\frac{c}{d}$ elemére $cb-ad=1$, így a $\frac{19}{99}$-hez tartozó maximális intervallum két végpontja $\frac{19}{99}$ két szomszédja lesz az ${\text{F}}_{99}$ sorozatban. Gáspár-Merse Előd (Fazekas M. Főv. Gyak. Gimn., 12. o.t.) ezzel a módszerrel kereste meg a szóban forgó intervallumot.