Feladat: C.555 Korcsoport: 14-15 Nehézségi fok: könnyű
Füzet: 2000/szeptember, 344. oldal  PDF  |  MathML 
Témakör(ök): Természetes számok, Négyzetszámok tulajdonságai, Osztók száma, Additív számelméleti problémák, C gyakorlat
Hivatkozás(ok):Feladatok: 1999/november: C.555

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen az N egész szám kétféle felbontása:

a2+b2=c2+d2=N,
ahol a, b, c, d pozitív egész számok, és például a>c, d>b.
Átrendezve és szorzattá alakítva az egyenlőséget, kapjuk, hogy
(a+c)(a-c)=(d+b)(d-b).

A négy tényező paritása megegyezik, mert ha (a+c) páratlan, akkor (a-c) is az, tehát szorzatuk is páratlan, így a jobb oldali két tényező ugyancsak páratlan lesz. Vagyis ebben az esetben N-nek 4 különböző pozitív páratlan osztója van. Hasonló mondható el a páros esetre is. Könnyű olyan kis egész számot találni, amelynek 4 különböző páratlan pozitív osztója van. Ha felírjuk sorban az egész számokat, és megnézzük, melyiknek hány osztója van, rögtön láthatjuk, hogy N=15 például ilyen; osztói: 1, 3, 5 és 15. Az osztók szorzatára az 1⋅15=3⋅5 egyenlőség áll fenn.
Mivel a+c>a-c; a+c=15, a-c=1, ahonnan a=8, c=7. Továbbá d+b>d-b miatt d+b=5, d-b=3, és innen d=4, b=1.
Valóban, N=82+12=72+42=65 megoldás.
Most már csak azt kell igazolnunk, hogy 65 a legkisebb egész szám, amely eleget tesz a követelménynek.
Ehhez készítsük el az x2+y2 összegek táblázatát 1<x,y≤8 esetére. A táblázatból leolvashatjuk, hogy a négyzetösszegek mind különbözők, kivéve az általunk már megkapott 65-öt.
 

Megjegyzés. A Gauss-egészek számelméletéből tudjuk, hogy az N szám pq alakú, ahol p és q a két legkisebb 4k+1 alakú pozitív prímszám, azaz 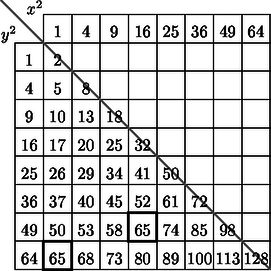p=3, q=13 és N=5⋅13=65.