Feladat:	B.3302	Korcsoport: 14-15	Nehézségi fok: könnyű
Megoldó(k):	Csötönyi Nóra
Füzet:	2000/április, 217 - 220. oldal		PDF  |  MathML
Témakör(ök):	Kombinatorikai leszámolási problémák, Egyéb ponthalmazok a koordinátasíkon, Konstruktív megoldási módszer, Feladat
Hivatkozás(ok):	Feladatok: 1999/október: B.3302

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Akkor nincsen fennakadás, ha bármeddig tekintjük is a sort, legalább annyian várakoznak 100 forintossal, mint 200 forintossal. Jelöljük az előbbieket $s$, utóbbiakat pedig $k$ betűvel, és számoljuk meg, hány olyan permutációja van a négy $s$ és négy $k$ betűnek, amikor nincsen fennakadás. Egy ilyen jó sorrendben az elsőnek érkező százassal, az utolsó pedig 200 forintossal kell fizessen, ezért egy tetszőleges jó sorrend $s\underline{}\underline{}\underline{}\underline{}\underline{}\underline{}k$ alakú. Csoportosítsuk a jó sorrendeket aszerint, hogy hányadik helyen áll az első néző, aki 200 forintossal akar fizetni. Ha ez $K$, akkor $2\le K\le 5$. (i) $K=5$. Egyetlen ilyen sorrend van: $sssskkkk$, és ez nyilván jó. (ii) $K=4$: $sssk\underline{}\underline{}\underline{}k$. A három lehetséges pozíció bármelyikére beírva a negyedik $s$ betűt, jó sorrendhez jutunk, így ebben az esetben 3 jó sorrendet kapunk. (iii) $K=3$: $ssk\underline{}\underline{}\underline{}\underline{}k$. A megmaradó két $s$ betűt $\left(\genfrac{}{}{0ex}{}{4}{2}\right)=6$-féleképpen írhatjuk a négy szabad pozíció közül kettőbe. E 6 sorrend közül csak 1 nem lesz jó, az, amikor a két $s$ betű az utolsó két szabad pozíción van. Ebben az esetben tehát 5 jó sorrendet kapunk. (iv) $K=2$: $sk\underline{}\underline{}\underline{}\underline{}\underline{}k$. A harmadik pozícióra ezután csak $s$ betű kerülhet, másképpen itt elakadna a sor: $sks\underline{}\underline{}\underline{}\underline{}k$. Így viszont lényegében az előző esethez, vagyis újabb 5 jó sorrendhez jutunk. Minden lehetőséget megvizsgálva összesen 14 jó sorrendet kaptunk. Mivel a 8 pozícióból $\left(\genfrac{}{}{0ex}{}{8}{4}\right)=70$-féleképpen választhatjuk ki azt a négyet, ahol $s$ betű áll, a pénztáros az összes sorrendek $\frac{14}{70}=\frac{1}{5}$-ében tudja csak fennakadás nélkül kiadni a jegyeket.   II. megoldás. Az előző megoldás jelöléseit használva most a ,,rossz'' sorrendeket számoljuk össze. Az elakadás előtt egyenlő számú $s$ és $k$ betű szerepel, az elakadás helyén pedig $k$ betű áll. Maga az elakadás így a $\left(2m+1\right)$-edik várakozónál következett be ($m=1$, 2, 3, 4). Módosítsuk most az ilyen sorozatokat a következőképpen: ha a $\left(2m+1\right)$-edik helyen kerül sor az elakadásra, akkor az első $\left(2m+1\right)$ pozíción az $s$ betűket cseréljük $k$ betűkre, a $k$ betűket pedig $s$-ekre. Az elakadás utáni pozíciókon ne változtassuk a betűket. $\begin{array}{c}{\displaystyle sskkk|\underline{}\underline{}\underline{}\to kksss|\underline{}\underline{}\underline{}\mathrm{.}}\end{array}$ Így olyan sorozathoz jutunk, amely 5 darab $s$ és 3 darab $k$ betűből áll. Megfordítva, ha tekintünk egy $\left(5s\mathrm{,}3k\right)$ sorozatot, akkor ebből egyértelműen kaphatunk egy rossz sorozatot: mivel több az $s$, mint a $k$, lesz egy legelső olyan pozíció, ahol az $s$ betűk többségbe kerülnek, és erre valamelyik páratlanadik pozíción kerül sor. Az $s\leftrightarrow k$ cserét eddig a pozícióig bezárólag elvégezve egy rossz sorozathoz jutunk. A rossz sorozatok száma így $\left(\genfrac{}{}{0ex}{}{8}{3}\right)=56$, a jó sorozatoké pedig $\left(\genfrac{}{}{0ex}{}{8}{4}\right)-56=14$.  Csötönyi Nóra (Bonyhád, Petőfi S. Gimn., 10. o.t.) dolgozata alapján   Megjegyzések. 1. A fenti leszámolásnak geometriai értelmezését is adhatjuk: egy-egy sorozatot az origóból induló töröttvonallal ábrázolhatunk: $s$ betű esetén az $\text{f}\left(\mathrm{1,}1\right)$, $k$ betű esetén pedig az $\text{l}\left(\mathrm{1,}-1\right)$ vektorral lépünk tovább. Így az origóból induló, a $\left(8;0\right)$ pontba érkező töröttvonalakat kapunk. Egy útvonal akkor rossz, ha érinti ‐ vagy metszi ‐ az $y=-1$ egyenest. A ,,rossz'' töröttvonalaknak az $y=-1$ egyenessel való első közös pontjáig haladó vektorok között hajtsuk végre az $\text{f}\leftrightarrow \text{l}$ cserét, így az origóból induló $\left(\mathrm{8,}2\right)$ pontban végződő útvonalhoz jutunk. Ilyen útvonal pedig $\left(\genfrac{}{}{0ex}{}{8}{3}\right)$ darab van. 2. A fenti ,,tükrözésnek'' egy másik, szemléletesebb végrehajtása és az ennek megfelelő leszámolás a következő: Tükrözzük egy $\left(\mathrm{0,}0\right)\to \left(8;0\right)$ rossz útvonalnak az $y=-1$ egyenessel való első közös pontja utáni részét az $y=-1$ egyenesre. Így a $\left(\mathrm{0,}0\right)$-ból induló $\left(\mathrm{8,}-2\right)$-ben végződő $\left(3s\mathrm{,}5k\right)$ útvonalhoz jutunk. Megfordítva, minden ilyen útvonal nyilván metszi az $y=-1$ egyenest; az első közös pontra tükrözve az út további részét egy rossz sorozatot kapunk. A rossz sorozatok száma tehát $\left(\genfrac{}{}{0ex}{}{8}{3}\right)$. 3. Bármelyik fenti módszerrel kapjuk, hogy ha a pénztár előtt $2n$ darab vevő várakozik, az egyik felük 100, másik felük pedig 200 forinttal, akkor az összes sorrendek száma $\left(\genfrac{}{}{0ex}{}{2n}{n}\right)$, a rosszaké pedig $\left(\genfrac{}{}{0ex}{}{2n}{n-1}\right)$. A pénztáros ilyenkor az összes sorrend $\frac{\left(\genfrac{}{}{0ex}{}{2n}{n}\right)-\left(\genfrac{}{}{0ex}{}{2n}{n-1}\right)}{\left(\genfrac{}{}{0ex}{}{2n}{n}\right)}=\frac{1}{n+1}$-edrészében tudja fennakadás nélkül kiadni a jegyeket. A tükrözéses módszerrel akkor is választ kapunk a feladat kérdésére, ha a 100 forintossal és 200 forintossal várakozók száma különböző. Ha $n$ néző várakozik 100 forintossal és $m$ 200 forintossal ($n\ge m$), akkor ugyanúgy kapjuk (3. ábra), hogy a rossz sorrendek száma 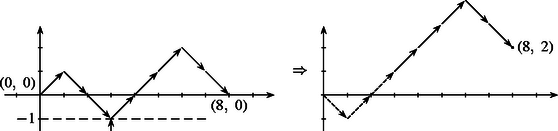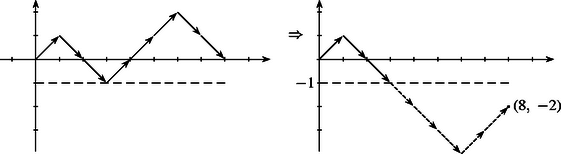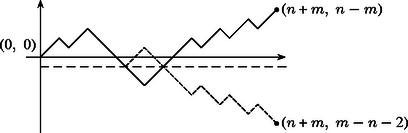$\left(\genfrac{}{}{0ex}{}{n+m}{m-1}\right)$.