Kezdőlap


Feladat:	N.176	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Bérczi Gergely , Kun Gábor
Füzet:	1999/március, 162 - 163. oldal		PDF \| MathML
Témakör(ök):	Algebrai egyenlőtlenségek, Mátrixjátékok, Nehéz feladat
Hivatkozás(ok):	Feladatok: 1998/május: N.176

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Alsó becslés: Először becsüljük meg, hogy egy $3 \times k$ -as téglalapnak legalább hány bejárása van:
$2^{k - 1}$ -féleképpen lehet felosztani 3 magasságú téglalapokra a táblát. Minden ilyen felosztáshoz tartozik egy bejárás, amit úgy kapunk, hogy a 3 magasságú szeleteket ,,S'', illetve ,,Z'' alakú úton járjuk be (1. ábra). Ezek mind különböző bejárások.
Vizsgáljuk most azt, hogy egy $3 \times n$ -es táblát hányféleképpen lehet úgy bejárni, hogy az átellenes sarok az utolsó mező. Vegyük az első $3 \times (n - 2)$ -es részt. Ezt bejárjuk tetszőlegesen, az utolsó $3 \times 2$ -es részben pedig úgy manőverezünk, hogy a megfelelő sarokba érkezzünk. Ez mindig lehetséges:
Az $n \times n$ -es táblán elhelyezünk $[\frac{n}{3}]$ kicsi táblát, amelyek $3 \times n$ -esek. Ezeket sorban bejárjuk a fenti módon, majd az alul esetleg kimaradó 1‐2 sort tetszőlegesen bejárjuk. Így $t_{n} \geq 2^{(n - 3) [\frac{n}{3}]}$ , és

\begin{matrix} \sqrt[n^{2}]{2^{(n - 3) [\frac{n}{3}]}} \to \sqrt[3]{2} > 1,25. \end{matrix}

Felső becslés: Tekintsünk egy adott bejárást. Két mezőt összekötünk, ha a bábu köztük lépett egyet a bejárás közben. Tegyük fel, hogy csak a párosadik oszlopokban levő mezőkről tudjuk, mely mezőkkel vannak összekötve. Azt állítjuk, hogy ezek már meghatározzák a bejárást, ha még azt is tudjuk, melyik mezőn ér véget az útvonal.
Bizonyítás: Minden mezőről tudjuk, hogy egy vagy két mezővel van-e összekötve a négy (vagy kevesebb) szomszédja közül. Ha egy rögzített mező szomszédairól egyet kivéve tudjuk, melyikkel van összekötve, melyikkel nem, akkor a hiányzóról kikövetkeztethetjük, vele össze van-e kötve a rögzített mező. Így a páratlanadik oszlopok fentről lefelé haladva egyértelműen ,,kitölthetők''.
Még azt számoljuk ki, hogy legfeljebb hányféleképpen lehet egy oszlopot úgy megrajzolni, hogy a 2. ábra egy bejárásából származhasson.
A legfelső mező legfeljebb 3-féleképpen tölthető ki, mert 1 vagy 2 él megy belőle 2 vagy 3 szomszédba. Ha egy mező felett már kitöltöttük a többit, akkor legfeljebb 3 lehetőség marad erre a mezőre, a fentihez hasonlóan. A legalsó mezőnél már csak legfeljebb 2 eset lehetséges. Azaz egy oszlop szóba jövő kitöltéseinek száma

2 \cdot 3^{n - 1}

.
(A fenti gondolatmenet akkor is működik, ha a kezdő vagy utolsó mező, aminek egy kimenő éle van, ebbe az oszlopba esik.)
Mivel

n^{2}

-féle lehet az utolsó mező, azért

\begin{matrix} n^{2} (3^{[\frac{n}{2}] \cdot (n - 1)} \cdot 2^{[\frac{n}{2}]}) \geq t_{n}, \sqrt[n^{2}]{t_{n}} \leq \sqrt[n^{2}]{n^{2} \cdot 3^{\frac{n^{2}}{2}}}, és \sqrt[n^{2}]{n^{2} \cdot 3^{\frac{n^{2}}{2}}} \to \sqrt[]{3} < 2. \end{matrix}

Megjegyzés. A fenti bizonyítás a felső becslésére Bérczi Gergely ötlete alapján történt.
Az alsó becslést Kun Gábor ennél élesebbre is kihozta, a megoldásából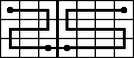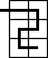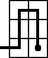

\begin{matrix} \sqrt[3]{2} < \sqrt[4]{\frac{3 + \sqrt[]{5}}{2}} < {lim inf}_{n}^{} \sqrt[n^{2}]{t_{n}} . \end{matrix}