Kezdőlap


Feladat:	N.167	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bérczi Gergely , Csóka Endre , Terpai Tamás , Végh A.László
Füzet:	1999/március, 160 - 162. oldal		PDF \| MathML
Témakör(ök):	Terület, felszín, Kör (és részhalmaza), mint mértani hely, Nehéz feladat
Hivatkozás(ok):	Feladatok: 1998/március: N.167

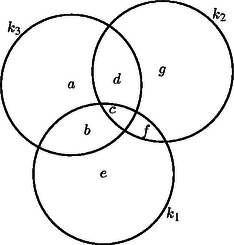
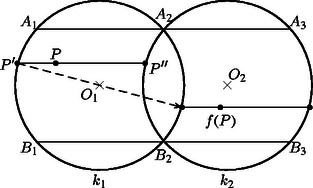
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a körök által háromszorosan lefedett területrészt $t_{3}$ -mal, és használjuk az 1. ábra jelöléseit (az $a$ , $b$ , $c$ , $d$ , $e$ , $f$ , $g$ a megfelelő tartományokat és azok területét is jelölik).
A feladat állítása: $t_{1} \geq t_{2}$ , azaz $3 π = t_{1} + 2 t_{2} + 3 t_{3}$ miatt $t_{2} + t_{3} \leq π$ . Ez $b + c + d + f \leq π$ , ami másképpen írva

\begin{matrix} b \leq π - c - d - f = g . \end{matrix}

Most nézzük a 2. ábrát (

A_{1} A_{2} A_{3} ‖ B_{1} B_{2} B_{3} ‖ O_{1} O_{2} ‖ P' P''

).
Megadunk egy

\begin{matrix} f : k_{1} ∖ k_{2} \to k_{2} ∖ k_{1} \end{matrix}

leképezést:

P \in k_{1} ∖ k_{2}

és

P

A_{1} A_{2}

és

B_{1} B_{2}

között található, akkor

f (P)

-t úgy kapjuk, hogy

P

-t eltoljuk

2 \vec{P' O_{1}}

-gyel;

ha pedig

P

például az

A_{1} A_{2}

körszeletben van, akkor egy olyan csúsztatva tükrözéssel kapjuk belőle

f (P)

-t, amely az

A_{1} A_{2}

szeletet a

B_{2} B_{3}

körszeletbe viszi. (Hasonlóan

f

B_{1} B_{2}

körszeletet az

A_{2} A_{3}

szeletbe képezi.) Ezzel minden

P \in k_{1} ∖ k_{2}

-re megadtuk

f (P)

-t.
A következő két állítás részletes bizonyítását az Olvasóra bízzuk:
a)

f

területtartó (Cavalieri-elv)
b) minden

P

-re

d (P, f (P))

(azaz

P

és

f (P)

távolsága) legalább 2.
Ezek szerint elég lenne belátnunk, hogy

f (b) \subset g

, mert akkor

b \leq g

bizonyítást nyer. Tegyük fel, hogy ez nem igaz, azaz van egy

B \in b

, amelyre

f (B) \notin g

; azaz

f (B) \in d

. Ekkor

B

és

f (B)

egyaránt benne vannak

k_{3}

-ban, és távolságuk legalább 2. Ez ellentmondás, hiszen nyugodtan feltehetjük, hogy nyílt körlapokkal van dolgunk.
Készen is lennénk, csak a bizonyítás során definiált

f

nem adható meg, ha a három kör között nincs két olyan, amely a 2. ábra szerint helyezkedik el, azaz ha a körök közül kettő egybeesik, vagy ha semelyik két körnek nincs közös pontja. Ezek az esetek viszont triviálisak.

Csóka Endre (Debrecen, Fazekas M. Gimn., 8. o.t.) megoldása alapján

Megjegyzés. Ez a megoldás működik akkor is, ha körök helyett egy szimmetrikus konvex síkidom három eltolt példányáról van szó, bár akkor egy-két rész nehezebben kezelhető.