Kezdőlap


Feladat:	B.3355	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	2000/december, 532 - 534. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai számítások trigonometria nélkül, Heron-képlet, Síkgeometriai bizonyítások, Pitagorasz-tétel alkalmazásai, Feladat
Hivatkozás(ok):	Feladatok: 2000/március: B.3355

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Közismert, hogy ha egy háromszög oldalai $a$ , $b$ , $c$ . kerülete $2 s$ , területe $T$ , beírt körének sugara $ϱ$ , a hozzáírt kör sugarai pedig $ϱ_{a}$ , $ϱ_{b}$ és $ϱ_{c}$ , akkor

\begin{matrix} ϱ \cdot s = ϱ_{a} (s - a) = ϱ_{b} (s - b) = ϱ_{c} (s - c) = T = \sqrt[]{s (s - a) (s - b) (s - c)} . \end{matrix}

(1)

(A képletek bizonyításának vázlata a megoldás utáni megjegyzésben olvasható.)
Elegendő megmutatnunk, hogy a

ϱ_{a} \cdot ϱ_{b} = T

és az

a^{2} + b^{2} = c^{2}

egyenlőségek ekvivalensek. Az (1) összefüggések szerint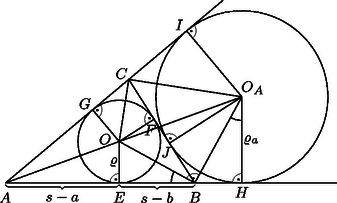

\begin{matrix} ϱ_{a} \cdot ϱ_{b} = \frac{T}{s - a} \cdot \frac{T}{s - b} = \frac{T^{2}}{(s - a) (s - b)} = s (s - c) . \end{matrix}

Látható, hogy

ϱ_{a} \cdot ϱ_{b} = T

pontosan akkor teljesül, ha

s (s - c) = \sqrt[]{s (s - a) (s - b) (s - c)}

, azaz ha

\begin{matrix} s (s - c) = (s - a) (s - b) . \end{matrix}

Mivel

2 s = a + b + c

, azért ez ekvivalens az

\begin{matrix} (a + b + c) (a + b - c) = (c - a + b) (c + a - b) \end{matrix}

egyenlőséggel. Elvégezve a szorzásokat

\begin{matrix} {(a + b)}^{2} - c^{2} = c^{2} - {(a - b)}^{2} \end{matrix}

adódik, amit rendezve és 2-vel osztva kapjuk az

a^{2} + b^{2} = c^{2}

összefüggést. Ez éppen az, amit bizonyítani akartunk, hiszen egy háromszög pontosan akkor derékszögű, ha két oldalhosszának négyzetösszege egyenlő a harmadik oldal hosszának négyzetével.

Megjegyzés. A képletek bizonyításához használjuk az ábra jelöléseit. Az

A B C

háromszög területe megegyezik az

O A B

O B C

és

O C A

háromszögek területének összegével. A három kis háromszög mindegyikében

ϱ

O

-ból induló magasság, amiből

2 T = c \cdot ϱ + b \cdot ϱ + a \cdot ϱ = 2 ϱ s

adódik. Ha az

O_{A} A B

és az

O_{A} A C

háromszögek területének összegéből kivonjuk az

O_{A} B C

háromszög területét, akkor szintén az

A B C

háromszög területét kapjuk. Az

O_{A}

-ból húzott mindhárom magasság

ϱ_{a}

, ezért

2 T = c \cdot ϱ_{a} + b \cdot ϱ_{a} - a \cdot ϱ_{a} = 2 ϱ_{a} (s - a)

. Ugyanígy látható be, hogy

ϱ_{b} (s - b) = T = ϱ_{c} (s - c)

.

Az

O B

egyenes az

A B C

háromszög

B

-hez tartozó belső-,

O_{A} B

pedig egyik külső szögfelezője, ezért

O B O_{A} ∢ = 90^{\circ}

. Tehát

O B E ∢ = B O_{A} H ∢

, mert merőleges szárú hegyesszögek. Így az

O B E

és a

B O_{A} H

derékszögű háromszögek hasonlóak, mert megfelelő szögeik egyenlők. Ezért a megfelelő oldalaik aránya is megegyezik:

\begin{matrix} \frac{ϱ}{E B} = \frac{B H}{ϱ_{a}} . \end{matrix}

(2)

Mivel egy körhöz egy külső pontból húzható két érintőszakasz hossza egyenlő, azért

A E = A G

B E = B F

és

C F = C G

. Másrészt

A E + B E = c

B F + C F = a

és

C G + A G = b

, amiből adódik, hogy pl.

B E = s - b

. Az

A I = A H

B H = B J

C J = C I

és az

A H - B H = c

A I - C I = b

és

B J + C J = a

egyenlőségekből pedig pl.

B H = s - c

következik. Vagyis a (2) egyenlőség szerint

\begin{matrix} \frac{ϱ}{s - b} = \frac{s - c}{ϱ_{a}} . \end{matrix}

Felhasználva a

ϱ = \frac{T}{s}

és a

ϱ_{a} = \frac{T}{s - a}

összefüggéseket kapjuk, hogy

\begin{matrix} \frac{T}{s (s - b)} = \frac{(s - c) (s - a)}{T}, \end{matrix}

amiből már egyszerűen adódik Héron képlete:

\begin{matrix} T = \sqrt[]{s (s - a) (s - b) (s - c)} . \end{matrix}