Kezdőlap


Feladat:	B.3354	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Ambrus Gergely , Béky Bence , Csernenszky András , Csikvári Péter , Kunszenti-Kovács Dávid , Pach Péter Pál , Sipos Ádám , Soproni Péter , Zavarkó Gábor
Füzet:	2000/október, 418 - 419. oldal		PDF \| MathML
Témakör(ök):	Mértani helyek, Síkgeometriai számítások trigonometriával, Feladat
Hivatkozás(ok):	Feladatok: 2000/március: B.3354

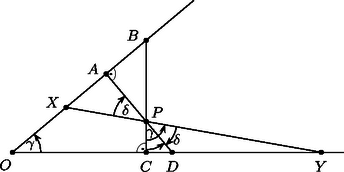
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A két egyenes metszéspontját jelöljük $O$ -val. Húzzunk $P$ -n keresztül az egyenesekre merőlegeseket, legyenek ezek $A D$ és $B C$ az 1. ábra szerint. Irányított szögekkel számolunk.

\begin{matrix} \begin{matrix} X P A ∢ ∢ + C P Y ∢ = \\ = Y P D ∢ + C P Y ∢ = C P D ∢, \end{matrix} \end{matrix}

ami az

X

Y

-tól független állandó, jelöljük az értékét

γ

-val. (Nyilván

C O A ∢ = C P D ∢ = γ

, mivel merőleges szárú szögek.)
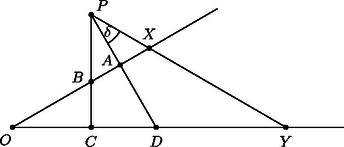
Jelöljük az

X P A

szöget

δ

-val, ekkor tehát

C P Y ∢ = γ - δ

, és az

X A P

P C Y

derékszögű háromszögekből

\begin{matrix} P X = \frac{A P}{cos δ}, P Y = \frac{C P}{cos (γ - δ)} . \end{matrix}

Így

P X \cdot P Y = \frac{A P \cdot C P}{cos δ \cdot cos (γ - δ)}

pontosan akkor minimális, ha

cos δ \cdot cos (γ - δ)

maximális. Mivel

cos δ \cdot cos (γ - δ) = \frac{1}{2} (cos γ + cos (2 δ - γ))

, azért

\begin{matrix} cos δ \cdot cos (γ - δ) \leq \frac{1}{2} (cos γ + 1) \end{matrix}

és egyenlőség lehetséges, ha

δ = \frac{γ}{2}

. A szerkesztendő pontokat tehát a

C P D

szög belső szögfelezője metszi ki az

O

csúcsszög száraiból. A szerkesztést ezzel egy szög felezésére vezettük vissza. Hasonlóan járhatunk el akkor is, ha

P

X

Y

által meghatározott szögtartomány külső pontja (2. ábra), illetve ha az

X O Y

szög tompaszög.

Pach Péter Pál (Fazekas M. Főv. Gyak. Gimn., 8. o.t.)

Sipos Ádám (Miskolc, Földes F. Gimn., 12. o.t.) és

Soproni Péter(Budapest, Szent István Gimn., 10. o.t.) dolgozatai alapján