Feladat: B.3343 Korcsoport: 16-17 Nehézségi fok: könnyű
Megoldó(k):  Szilágyi Örs 
Füzet: 2000/október, 414 - 416. oldal  PDF  |  MathML 
Témakör(ök): Síkgeometriai bizonyítások, Párhuzamos szelők tétele és megfordítása, Háromszögek geometriája, Vektorok felbontása összetevőkre, Feladat
Hivatkozás(ok):Feladatok: 2000/február: B.3343

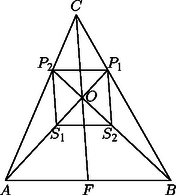
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

 
I. megoldás. Legyen a CF szakasz felezőpontja O. Mivel S1 és S2 súlypontok, azért harmadolják a súlyvonalakat, vagyis az OA1, illetve az OB szakaszokat is. Ebből következik, hogy S1S2 párhuzamos AB-vel, és S1S2=13AB. Alkalmazzuk Menelaosz tételét (bizonyítását lásd pl. Geometriai feladatok gyűjteménye, I. kötet, 1260. feladat) az AFC háromszögre és a BP2 egyenesre:
CP2P2A⋅ABBF⋅FOOC=-1.
F az AB, O pedig az FC szakasz felezőpontja, ezért az előző összefüggésből ABBF=-2 és FOOC=1 miatt CP2P2A=12 következik, vagyis P2 az AC szakasz C-hez közelebbi harmadolópontja. Ugyanígy kapjuk, hogy P1 a BC szakasz C-hez közelebbi harmadolópontja, ha Menelaosz tételét a BFC háromszögre és az AP1 egyenesre alkalmazzuk. Ez viszont azt jelenti, hogy az AB szakaszt C-ből 13 arányban kicsinyítve a P2P1 szakaszt kapjuk. Ezért P2P1‖AB‖S1S2 és P2P1=13AB=S1S2. Tehát az S1S2P1P2 négyszög paralelogramma, mert két szemközti oldala párhuzamos és egyenlő.
 Szilágyi Örs (Miskolc, Földes F. Gimn., 10. o.t.) dolgozata alapján

 
 

 
II. megoldás. Legyen a CF szakasz O felezőpontjából A-ba mutató vektor 6a, B-be mutató vektor pedig 6b. Mivel F az AB felezőpontja, azért OF→=12(OA→+OB→)=3a+3b; O pedig a CF felezőpontja, ezért OC→=-OF→=-3a-3b. Az OA, illetve OB szakaszok súlyvonalak, amit a megfelelő súlypontok harmadolnak, ezért
OS1→=13OA→=2aésOS2→=13OB→=2b.

 
 

A CA szakasz C-hez közelebbi H2 harmadolópontjába mutató vektor az ismert képlet szerint:
OH2→=13(2OC→+OA→)=13(-6a-6b+6a)=-2b.
Vagyis OH2→=-OS2→, ami azt jelenti, hogy H2 rajta van az OS2 egyenesen is, ezért megegyezik OS2 és AC metszéspontjával, vagyis P2-vel. Tehát OP2→=-2b.
Ugyanígy kapjuk, hogy OP1→=-2a. Vagyis OP1→=-OS1→ és OP2→=-OS2→, tehát az S1S2P1P2 négyszögnek O szimmetriaiközéppontja. Ezért a négyszög paralelogramma.