Kezdőlap


Feladat:	3109. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Füzet:	1998/február, 122 - 123. oldal		PDF \| MathML
Témakör(ök):	Egyéb merev test térbeli mozgása, Csúszásmentes (tiszta) gördülés, Feladat
Hivatkozás(ok):	Feladatok: 1997/november: 3109. fizika feladat

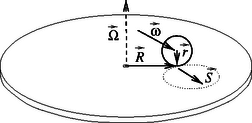
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Írjuk le a labda mozgását az ,,álló'' (a lemezjátszó dobozához rögzített) koordináta-rendszerből nézve. Jelöljük a labda tömegközéppontjának sebességét $\vec{v}$ -vel, gyorsulását $\vec{a}$ -val, a labda forgási szögsebességét $\vec{ω}$ -val, szöggyorsulását $\vec{β}$ -val, a síklap által kifejtett súrlódási erőt pedig $\vec{S}$ -sel. Ezek a mennyiségek vízszintes irányú vektorok. (A labda függőleges tengely körül is foroghat, ha kezdetben volt ilyen irányú szögsebessége, de ez a mozgás független a többitől, ezért a továbbiakban nem foglalkozunk vele.) Érdemes bevezetni még két további jelölést: labda középpontjából a legalsó pontjába lefelé mutató $\vec{r}$ vektort, valamint a korong $\vec{Ω}$ szögsebesség-vektorát. (Mindkét vektor függőleges irányú és időben állandó.)
Ezekkel a vektormennyiségekkel tömör alakban felírhatjuk az $m$ tömegű, $Θ$ tehetetlenségi nyomatékú labda mozgásegyenleteit. A dinamika alaptörvénye szerint

\begin{matrix} \vec{S} = m \vec{a}, \end{matrix}

(1)

a forgómozgás alaptörvénye szerint pedig

\begin{matrix} \vec{r} \times \vec{S} = Θ \vec{β} . \end{matrix}

(2)

A labda tisztán gördül a síklapon, legalsó pontjának sebessége tehát ugyanakkora, mint az érintkezésnél a síklap megfelelő (a lemezjátszó tengelyétől kiinduló

\vec{R}

vektorral jellemzett) pontjának sebessége. Mivel a labda legalsó pontjának sebessége a tömegközéppont

\vec{v}

sebességének és a forgásból származó

\vec{ω} \times \vec{r}

kerületi sebességnek összege, a síklap megfelelő pontjának sebessége pedig

\vec{Ω} \times \vec{R}

, a csúszásmentes gördülés feltétele:

\begin{matrix} \vec{v} + (\vec{ω} \times \vec{r}) = \vec{Ω} \times \vec{R} . \end{matrix}

(3)

Képezzük a (3) egyenletben szereplő mennyiségek változási sebességét! Mivel

\vec{Ω}

és

\vec{r}

időben állandó vektorok,

\vec{R}

változási sebessége pedig éppen a labda

\vec{v}

sebességvektora, írhatjuk, hogy

\begin{matrix} \vec{a} + (\vec{β} \times \vec{r}) = \vec{Ω} \times \vec{v} . \end{matrix}

(4)

Fejezzük ki (1)-ből az

\vec{S}

vektort és helyettesítsük be (2)-be, majd onnan fejezzük ki

\vec{β}

-t és írjuk be (4)-be:

\begin{matrix} \vec{a} + \frac{m}{Θ} [(\vec{r} \times \vec{a}) \times \vec{r}] = \vec{Ω} \times \vec{v} . \end{matrix}

(5)

A szögletes zárójelben álló vektor

\vec{a}

és

\vec{r}

merőlegessége miatt

r^{2} \cdot \vec{a}

(ahol

r

a labda sugara), továbbá

Θ = \frac{2}{5} m r^{2}

felhasználásával (5) ilyen alakra hozható:

\begin{matrix} \vec{a} + \frac{5}{2} \vec{a} = \vec{Ω} \times \vec{v}, azaz \vec{a} = \frac{2}{7} \vec{Ω} \times \vec{v} . \end{matrix}

(6)

Ez az egyenlet azt mutatja, hogy a labda sebességvektora

\frac{2}{7} Ω

szögsebességgel egyenletesen forog körbe, a labda tömegközéppontja tehát ilyen szögsebességű egyenletes körmozgást végez. A körpálya középpontja általában nem esik egybe a lemezjátszó tányérjának közepével, hanem a kezdőfeltételektől (az indítás helyétől és a kezdősebességtől) függően máshol is lehet.

Megjegyzések: 1. Vigyázat: a merev testek térbeli forgómozgásának egyenlete általában nem olyan ,,egyszerű'', mint ahogy az a (2) egyenletben szerepel, hanem csak a perdület vektorának változási sebességével fogalmazható meg. Jelen esetben (a labda gömbszimmetriája miatt) a perdület

Θ \cdot \vec{ω}

alakú, s ennek változási sebessége (mivel

Θ

nem csak a testhez rögzített rendszerből, de az inerciarendszerből nézve is állandó)

Θ \vec{β}

.
2. A labda tömegközépponti szögsebességének és a lemezjátszó szögsebességének aránya a jelen esetben (tömör, homogén lábdánál)

\frac{2}{7}

, általában pedig

\frac{Θ}{Θ + m r^{2}} .

Vékonyfalú labdánál (teniszlabda, pingponglabda) például

Θ = \frac{2}{3} m r^{2},

ilyenkor a legnagyobb a két szögsebesség aránya, nevezetesen

\frac{2}{5}

(G. P.)