Feladat:	Gy.3275	Korcsoport: 14-15	Nehézségi fok: könnyű
Megoldó(k):	Bálint Gergely ,  Balka Richárd ,  Deli Lajos ,  Fischer Noémi ,  Horváth Balázs ,  Horváth Szilárd ,  Nagy Zoltán ,  Rácz Judit ,  Zalán Péter
Füzet:	2000/április, 215. oldal		PDF  |  MathML
Témakör(ök):	Terület, felszín, Paralelogrammák, Síkgeometriai bizonyítások, Négyszögek geometriája, Gyakorlat
Hivatkozás(ok):	Feladatok: 1999/április: Gy.3275

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. A feltételből következik, hogy négyszög konvex. Használjuk az 1. ábra jelöléseit! $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{c}\hfill {\displaystyle t_1=\frac{1}{2}xn\mathrm{,}{t}_2=\frac{1}{2}xm\mathrm{,}{t}_3=\frac{1}{2}ym\mathrm{,}{t}_4=\frac{1}{2}yn\mathrm{.}}\end{array}}}\end{array}$ Ebből látható, hogy $t_1{t}_3=t_2{t}_4$. Az átlók felezik a területet, azaz $t_1+t_2=t_3+t_4$, és $t_1+t_4=t_2+t_3$. E két egyenlőség összeadásából $t_1=t_3$, ezért $t_2=t_4$. A területek szorzatára kapott egyenlőségek szerint így $t_1^2=t_2^2$, tehát $t_1=t_2$. Innen pedig azonnal adódik, hogy mind a négy terület egyenlő.  Fischer Noémi (Budapest, Árpád Gimn., 9. o.t.)   II. megoldás. Belátjuk, hogy a feltétel teljesülésekor a négyszög paralelogramma. Tegyük fel, hogy nem az, vagyis valamelyik átló nem felezi a másikat, például a $BD$ átló $F$ felezőpontja nem esik $AC$-re, hanem pl. az $ABC$ háromszög belsejében van (2. ábra). Az $AF$ súlyvonal felezi $ABD$ területét, $FC$ pedig $BCD$-ét. Ebből adódik, hogy $t_{ABF}+t_{BCF}$ a négyszög területének a fele, ami egyenlő $t_{ABC}$-vel. A két felírt terület különbségeként azt kapjuk, hogy $t_{AFC}=0$, ami azt jelenti, hogy az átlók felezik egymást. Az $ABCD$ négyszög tehát paralelogramma, amelyben az átlók által létrehozott négy háromszög területe nyilván egyenlő.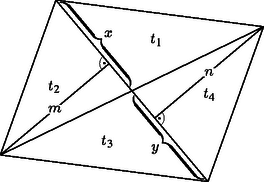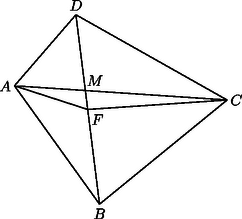