Kezdőlap


Feladat:	B.3299	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Csóka Endre
Füzet:	2000/március, 160 - 161. oldal		PDF \| MathML
Témakör(ök):	Terület, felszín, Körök, Egyenlőtlenségek, Feladat
Hivatkozás(ok):	Feladatok: 1999/szeptember: B.3299

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Mivel minden érme egy teljes lapjával az asztalon fekszik, azért az érmék lapjának összterülete legfeljebb akkora, mint az asztallap területe, azaz $n \cdot r^{2} π \leq R^{2} π$ . Ebből rendezéssel kapjuk a

\begin{matrix} \sqrt[]{n} \leq \frac{R}{r} \end{matrix}

egyenlőtlenséget.
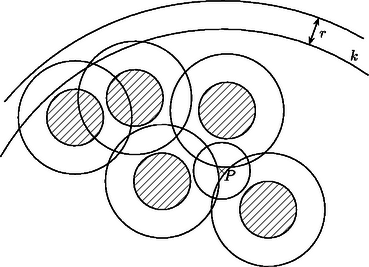
Rajzoljunk az érmék középpontjai körül

2 r

sugarú köröket, az asztal középpontja körül pedig egy

R - r

sugarú

k

kört. Ha ennek a

k

körnek lenne egy olyan

P

pontja, amit a

2 r

sugarú körök egyike sem tartalmaz, akkor a

P

középpontú

r

sugarú kör egyik érmét sem metszené, és teljes egészében az asztalon volna (lásd az ábrát). Vagyis egy újabb érmét helyezhetnénk az asztalra úgy, hogy középpontja egybeesne

P

-vel. A feladat feltételei szerint ez nem lehetséges, ezért a

2 r

sugarú körök teljes egészében lefedik

k

-t. Emiatt a területük legalább akkora, mint

k

területe:

\begin{matrix} {(R - r)}^{2} \cdot π \leq n {(2 r)}^{2} \cdot π . \end{matrix}

Ezt átrendezve éppen a bizonyítandó

\begin{matrix} \frac{1}{2} (\frac{R}{r} - 1) \leq \sqrt[]{n} \end{matrix}

egyenlőtlenséget kapjuk.

Csóka Endre (Debrecen, Fazekas M. Gimn., 9. o.t.) dolgozata alapján