|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Legyen a tizenkét szám ebben a sorrendben , , , , az egymás melletti számhármasok összege pedig , , , . Ezek összege, . Az összegek átlaga így , van tehát köztük legalább ekkora. Másfelől ezek az összegek egész számok, azért valóban van köztük olyan, amelyiknek legalább 20 az értéke.
Azt állítjuk, hogy a feladat második kérdésére is igenlő a válasz, az összegek között van 20-nál nagyobb is.
Tegyük fel, hogy ez nem igaz, a 12 szám elrendezhető úgy, hogy ne legyen 20-nál nagyobb összeg. Ha hatnál kevesebb 20 értékű összeg volna, akkor a tizenkét összeg összege legfeljebb lenne, ami lehetetlen. A 20 értékű összegek száma így legalább 6. Ha 7 vagy ennél is több ilyen összeg van, akkor van köztük két szomszédos, azaz . Szomszédos összegek értéke viszont egyáltalán nem lehet egyenlő, hiszen ebből következne.
Ha pontosan 6 maximális összeg van, akkor ahhoz, hogy 234 legyen a 12 számhármas összegének az összege, a további 6 számhármas mindegyikének összege 19 kell legyen.
A szomszédos összegek között nincsenek egyenlők, így a 12 számhármasban felváltva követik egymást a 19 és a 20 értékű összegek. Megmutatjuk, hogy ez nem lehetséges, feltétlenül van két szomszédos összeg, amelyek eltérése nagyobb, mint 1.
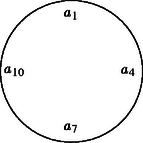
Tekintsük ehhez az , , , számokat (1. ábra). E négy szám különböző, így van köztük az adott körüljárás szerint szomszédos kettő, amelyek eltérése legalább 2. Például . Ez az eltérés viszont nem más, mint . E két szomszédos összeg eltérése így legalább 2, ami ellentmond a korábbiakban talált egyedül lehetséges elrendezésnek. Nem lehetséges tehát, hogy az összegek maximuma 20 legyen, van olyan összeg, amelyik legalább 21. A 2. ábrán látható elrendezésben az összegek maximuma éppen 21, eredményünk ezért tovább nem javítható.
| Tran Thanh Long (Fazekas M. Főv. Gyak. Gimn., 9. o.t.) dolgozata alapján |
|
 PDF |
PDF |  MathML
MathML