Kezdőlap


Feladat:	C.548	Korcsoport: 18-	Nehézségi fok: könnyű
Megoldó(k):	Vanya Ádám
Füzet:	2000/február, 85 - 86. oldal		PDF \| MathML
Témakör(ök):	Két pont távolsága, szakasz hosszúsága, Ponthalmazok távolsága, Koordináta-geometria, C gyakorlat
Hivatkozás(ok):	Feladatok: 1999/szeptember: C.548

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Alakítsuk szorzattá az egyenlet bal oldalát: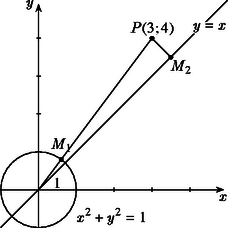

\begin{matrix} y (x^{2} + y^{2}) - x (x^{2} + y^{2}) - y + x = (y - x) (x^{2} + y^{2} - 1) = 0. \end{matrix}

Az első tényező az első síknegyedben az origón átmenő szögfelező egyenes egyenlete, a második az origó középpontú, egységnyi sugarú kör egyenlete. Az egyenletet a két ponthalmaz egyesítésében lévő pontok elégítik ki.

P

pontnak a körtől való távolsága az a szakasz, amelyet a

P

pont és a

P

-t az origóval összekötő szakasznak a körrel való

M_{1}

metszéspontja határoz meg. Ez a legrövidebb a

P

-t a kör kerületével összekötő szakaszok közül.

P

és

M_{1}

távolsága

d_{1} = \sqrt[]{3^{2} + 4^{2}} - 1 = 4

egység.
Egy pontból egy rajta át nem menő egyenes pontjaihoz húzott szakaszok közül a legrövidebb a merőleges szakasz. Számítsuk ki ennek a hosszát.

P

-ből az

y = x

egyenesre bocsátott merőleges egyenlete:

\begin{matrix} y - 4 = - (x - 3), rendezve y = - x + 7. \end{matrix}

A két egyenes metszéspontjának koordinátái a két egyenes egyenletéből

M_{2} (3,5; 3,5)

, és végül a két pont,

P

és

M_{2}

távolsága

\begin{matrix} d_{1} = \sqrt[]{{(3 - 3,5)}^{2} + {(4 - 3,5)}^{2}} = \frac{\sqrt[]{2}}{2} \approx 0,7071, \end{matrix}

ami kisebb, mint

d_{1} = 4

.
Tehát az egyenlettel megadott ponthalmaznak az

M_{2} (3,5; 3,5)

pontja van a

P

-hez legközelebb.

Vanya Ádám (Esztergom, Dobó K. Gimn., 11. o.t.)