Kezdőlap


Feladat:	F.3253	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1999/december, 534 - 535. oldal		PDF \| MathML
Témakör(ök):	Körérintési szerkesztések, Feladat
Hivatkozás(ok):	Feladatok: 1998/november: F.3253

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Vegyük fel $k$ -n az $E_{1}$ , $E_{2}$ , $E_{3}$ és $E_{4}$ pontokat úgy, hogy az $E_{1} E_{4}$ , $E_{2} P$ és $E_{3} P$ egyenesek egyike se menjen át $k$ középpontján, továbbá az $E_{1} E_{2}$ és $E_{4} P$ egyenesek $M$ metszéspontját az $E_{3} E_{4}$ és a $P E_{1}$ egyenesek $N$ metszéspontjával összekötő egyenes ne legyen párhuzamos az $E_{2} E_{3}$ egyenessel (lásd az ábrát). Ilyen pontok nyilván léteznek $k$ -n.
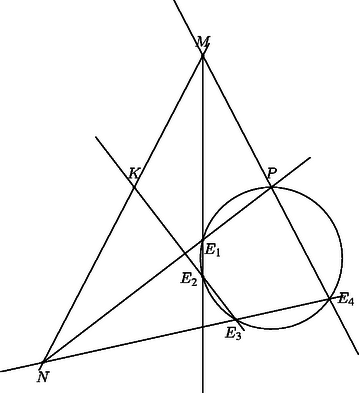
Az $E_{1}$ , $E_{2}$ , $E_{3}$ és $E_{4}$ pontok felvétele után az $M$ és az $N$ pontokat egyetlen vonalzó segítségével könnyen megszerkeszthetjük. Ezután szerkesszük meg az $M N$ és az $E_{2} E_{3}$ egyenesek $K$ metszéspontját, végül kössük össze $K$ -t $P$ -vel. Azt állítjuk, hogy a $K P$ egyenes a $k$ kör $P$ -beli érintője. Alkalmazzuk Pascal tételét a $k$ -ba írt $E_{1} E_{2} E_{3} E_{4} P P$ elfajult hatszögre. A tétel szerint a hatszög szemközti oldalpárjainak metszéspontjai egy egyenesre illeszkednek (az elfajuló $P P$ oldal éppen $k$ $P$ -beli érintője). Tehát az $E_{1} E_{2} \cap E_{4} P = M$ , az $E_{3} E_{4} \cap P E_{1} = N$ és az $E_{2} E_{3}$ egyenesnek $k$ $P$ -beli érintőjével alkotott metszéspontjai egy egyenesen vannak. Ezt úgy is fogalmazhatjuk, hogy az $M N$ egyenesnek és az $E_{2} E_{3}$ egyenesnek a metszéspontján átmegy $k$ $P$ -beli érintője, ami szerkesztésünk helyességét bizonyítja.