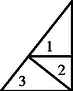
Azt bizonyítjuk be, hogy az arány csak ${\lambda }_1=1$ és ${\lambda }_2=\sqrt[]{\frac{\sqrt[]{5}+1}{2}}$ lehet. Itt ${\lambda }_1$ az egyenlő szárú derékszögű háromszög befogóaránya, ${\lambda }_2$ pedig az egyetlen olyané, amit az 1. ábra szerint felvágva az 1-es és 3-as darab egybevágó lesz. (Ezt egyszerűen ki lehet számolni.)
Először belátjuk, hogy ${\lambda }_1$, illetve ${\lambda }_2$ arányok esetén valóban mindig lesz két egybevágó darab minden vágás után.
Ha ${\lambda }_1$ az arány, akkor minden vágás két egybevágó egyenlő szárú derékszögű részre oszt, így az utolsó vágás mindig szolgáltat két egybevágó háromszöget.
Ha ${\lambda }_2$ az arány, akkor tegyük fel, hogy sikerült úgy vágni, hogy a végén csupa különböző darab keletkezett. Válasszuk ki a legrövidebb (legkevesebb vágásból álló) ilyen vágássorozatot! Vegyük észre még azt, hogy nem számít a vágások sorrendje.
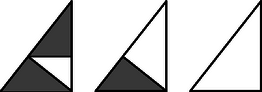
A három eredeti háromszög közül kettőt biztosan kettévágtunk. Nézzük a két vágás során keletkezett két nagyobbik darabot. Ezek közül az egyiket biztosan ketté kellett vágni. Így van három egybevágó, az eredetihez hasonló háromszög (2. ábra). Felejtsük el a többit részt, és folytassuk csak ezeken az eltervezett vágásokat. Az eljárás végén a feltevésünk szerint csupa különböző darab lesz. A három kisebb darabon tehát kevesebb vágás is elég volt, ez pedig ellentmondás, hiszen feltettük azt is, hogy egy minimális vágássorozatból indultunk ki.
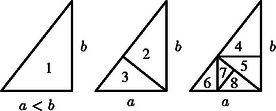
Most megmutatjuk, hogy ha a befogók aránya különbözik ${\lambda }_1$-től és ${\lambda }_2$-től, akkor a 3. ábrán jelölt vágások után kapott nyolc hasonló háromszög között nincsenek egybevágók. A tömörség kedvéért az alábbiakban $H_i$ egyszerre jelöli az ábrán $i$-vel jelölt számozott háromszöget, ennek területét, illetve a háromszög pontjaiból álló halmazt.
Ha két háromszögnek az ábrán van közös oldala, akkor területük nagyságviszonya eldönthető: az a kisebbik, ahol ez a közös oldal átfogó, illetve ahol ez a közös oldal a nagyobbik befogó, hiszen háromszögeink hasonlók.
Így kapjuk az alábbi egyenlőtlenségláncot: