Kezdőlap


Feladat:	C.522	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Ábrány Zsolt , Bérces Márton , Fehér Gergely , Robotka Zsolt , Strobl Apolka
Füzet:	1999/december, 516 - 518. oldal		PDF \| MathML
Témakör(ök):	Kúpszeletek érintői, Parabola egyenlete, C gyakorlat
Hivatkozás(ok):	Feladatok: 1998/december: C.522

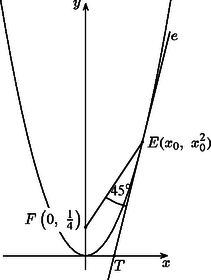
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Tudjuk, hogy az $y = \frac{1}{2 p} x^{2}$ másodfokú függvény görbéje egy olyan parabola, amelynek szimmetriatengelye az $y$ tengely, csúcsa az origóban van, és felfelé nyitott. A parabola paramétere $p$ , a fókuszpontnak a $d$ vezéregyenestől való távolságát méri. Esetünkben $y = x^{2}$ , azaz $\frac{1}{2 p} = 1$ , $p = \frac{1}{2}$ , a fókuszpont koordinátái $F (0; \frac{1}{4})$ . Legyen $E$ egy érintési pont (most csak az első síknegyedben vizsgáljuk az érintőket), az $E$ koordinátái $(x_{0}; x_{0}^{2})$ . Annak az $e$ érintőnek az egyenletét keressük, amely az $E F$ egyenessel $45^{\circ}$ -os szöget zár be.
Írjuk fel először az $E F$ egyenes egyenletét. $E F$ egy irányvektorának koordinátái $V (x_{0}; x_{0}^{2} - \frac{1}{4})$ ; egy pontjának koordinátái $F (0; \frac{1}{4})$ , így $E F$ egyenlete:

\begin{matrix} y = \frac{x_{0}^{2} - \frac{1}{4}}{x_{0}} x + \frac{1}{4} . \end{matrix}

Ismeretes, hogy a parabola érintőjének általános egyenlete:

\begin{matrix} x x_{0} = p (y + y_{0}), \end{matrix}

ahol

x_{0}

y_{0}

az érintési pontok koordinátái és

p

a paraméter.
Esetünkben

p = \frac{1}{2}

, így az érintő egyenlete:

x x_{0} = \frac{1}{2} (y + x_{0}^{2})

. Rendezve:

\begin{matrix} y = 2 x_{0} x - x_{0}^{2} . \end{matrix}

(1)

Ha az

m_{1}

m_{2}

iránytangensű egyenesek nem merőlegesek egymásra, akkor

α

hajlásszögükre a

\begin{matrix} tg α = | \frac{m_{1} - m_{2}}{1 + m_{1} m_{2}} | \end{matrix}

egyenlőség áll fenn. (Lásd pl. Hajós György: Bevezetés a geometriába c. könyv 339. oldal.)

\begin{matrix} tg 45^{\circ} = 1, m_{1} = \frac{x_{0}^{2} - \frac{1}{4}}{x_{0}}, m_{2} = 2 x_{0} \end{matrix}

helyettesítéssel kapjuk, hogy

\begin{matrix} 1 = | \frac{\frac{x_{0}^{2} - \frac{1}{4}}{x_{0}} - 2 x_{0}}{1 + \frac{x_{0}^{2} - \frac{1}{4}}{x_{0}} \cdot 2 x_{0}} | . \end{matrix}

x_{0} > 0

figyelembevételével rendezve:

\begin{matrix} \begin{matrix} 2 x_{0}^{3} + \frac{1}{2} x_{0} & = x_{0}^{2} + \frac{1}{4}, \\ ahonnan \\ 2 x_{0} (x_{0}^{2} + \frac{1}{4}) & = x_{0}^{2} + \frac{1}{4}, \\ x_{0}^{2} + \frac{1}{4} > 0-val végigosztva \\ 2 x_{0} & = 1, \\ x_{0} & = \frac{1}{2} . \end{matrix} \end{matrix}

Vagyis az

E

érintési pont koordinátái

(\frac{1}{2}; \frac{1}{4})

az első negyedben;

(- \frac{1}{2}; \frac{1}{4})

a második negyedben. Ezeket az értékeket helyettesítve (1)-be a keresett két érintő egyenlete:

y = x - \frac{1}{4}

, illetve

y = - x - \frac{1}{4}

Megjegyzés. A feladatot másképpen is megoldhatjuk, pl. úgy, hogy meghatározzuk az

e

érintő és az

x

tengely

T

metszéspontjának a koordinátáit, és az

F E T

háromszögre felírjuk a koszinusztételt, ahonnan

x_{0}

értéke kiszámítható.