Kezdőlap


Feladat:	F.3255	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Gerencsér Balázs , Lábó Eszter , Lábó Melinda , Székelyhidi Gábor
Füzet:	1999/november, 483 - 485. oldal		PDF \| MathML
Témakör(ök):	Gömb és részei, Feladat
Hivatkozás(ok):	Feladatok: 1998/november: F.3255

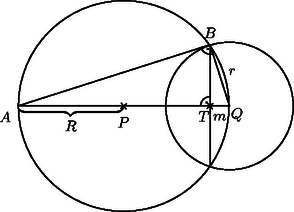
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Először kiszámoljuk, hogy egy $R$ sugarú gömb $S$ felszínének mekkora részét fedi le egy olyan $r$ sugarú ( $0 \leq r \leq 2 R$ ) $G$ gömb, amelynek középpontja $S$ -en van. A két gömb metszésvonala egy $k$ kör. Ha $k$ síkjának és $G$ középpontjának a távolságát $m$ -mel jelöljük, akkor a $G$ által $S$ -ből lefedett gömbsüveg felszíne az ismert képlet alapján $2 R \cdot π \cdot m$ (1. ábra). Tudjuk, hogy $S$ , $G$ és $k$ középpontjai ‐ jelöljük ezeket rendre $P$ , $Q$ , $T$ -vel ‐ egy egyenesre illeszkednek. Tekintsünk egy olyan síkmetszetet, amely tartalmazza ezt az egyenest (2. ábra). Az ábrán látható $A B Q$ háromszög Thalész tétele szerint derékszögű, így alkalmazhatjuk a befogótételt: $B Q^{2} = A Q \cdot T Q$ , azaz $r^{2} = 2 R \cdot m$ . Tehát a $G$ által $S$ felszínéből lefedett gömbsüveg felszíne $r^{2} \cdot π$ .
Jelöljük ezután a feladatban szereplő négy gömb sugarát $r_{1}$ , $r_{2}$ , $r_{3}$ , $r_{4}$ -gyel. Mivel a négy gömb páronként diszjunkt, az általuk lefedett felszín az előzőek alapján $(r_{1}^{2} + r_{2}^{2} + r_{3}^{2} + r_{4}^{2}) \cdot π$ . Az egység sugarú gömb felszíne $4 π$ , így azt kell igazolnunk, hogy

\begin{matrix} r_{1}^{2} + r_{2}^{2} + r_{3}^{2} + r_{4}^{2} \geq 1. \end{matrix}

Tudjuk, hogy

r_{1} + r_{2} + r_{3} + r_{4} = 2

; a számtani és a négyzetes közép közötti egyenlőtlenséget alkalmazva:

\begin{matrix} r_{1}^{2} + r_{2}^{2} + r_{3}^{2} + r_{4}^{2} \geq 4 \cdot {(\frac{r_{1} + r_{2} + r_{3} + r_{4}}{4})}^{2} = 4 \cdot \frac{1}{4} = 1. \end{matrix}

Ezzel a bizonyítandó állítást beláttuk.