Kezdőlap


Feladat:	F.3260	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Koch Dénes
Füzet:	1999/október, 419 - 420. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai bizonyítások, Esetvizsgálat, Feladat
Hivatkozás(ok):	Feladatok: 1998/december: F.3260

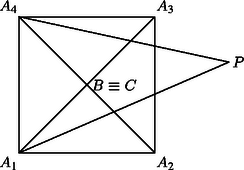
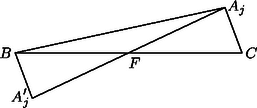
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az állítás nem igaz, ha $B$ és $C$ egybeesik. Legyen például $n = 4$ , az $A_{1}$ , $A_{2}$ , $A_{3}$ , $A_{4}$ pontok alkossanak négyzetet, $B$ és $C$ pedig essen egybe ezen négyzet átlóinak metszéspontjával. Ekkor a háromszög-egyenlőtlenség miatt a sík minden $P$ pontjára igaz, hogy $A_{1} P + A_{3} P \geq A_{1} A_{3} = A_{1} B + A_{3} B$ és $A_{2} P + A_{4} P \geq A_{2} A_{4} = A_{2} B + A_{4} B$ (1. ábra), tehát

\begin{matrix} \sum_{i = 1}^{4} A_{i} P \geq \sum_{i = 1}^{4} A_{i} B = \sum_{i = 1}^{4} A_{i} C . \end{matrix}

Megmutatjuk, hogy ha viszont

B

és

C

különböző pontok, akkor igaz az állítás. Tegyük fel ennek az ellenkezőjét. Ekkor az

A_{1}

A_{2}

...

A_{n}

pontok nincsenek mind egy egyenesen, ezért biztosan van köztük egy olyan

A_{j}

pont, amelyik nincs rajta a

B C

egyenesen. Legyen a

B C

szakasz felezőpontja

F

A_{j}'

pedig

A_{j}

-nek az

F

-re vonatkozó tükörképe (2. ábra). Ekkor a tükrözés miatt

A_{j} C = A_{j}' B

, és így az

A_{j} B A_{j}'

nem-elfajuló háromszög oldalaira felírva a háromszög-egyenlőtlenséget kapjuk, hogy

\begin{matrix} A_{j} B + A_{j} C = A_{j} B + A_{j}' B > A_{j} A_{j}' = 2 A_{j} F . \end{matrix}

Hasonló módon kapjuk, hogy minden

A_{i}

pont esetén

\begin{matrix} A_{i} B + A_{i} C \geq 2 A_{i} F, \end{matrix}

(egyenlőség csak akkor lehet, ha

A_{i}

rajta van a

B C

egyenesen). Ezeket összeadva és felhasználva, hogy az

A_{j}

pontra vonatkozó egyenlőtlenségben soha nincs egyenlőség, kapjuk, hogy

\begin{matrix} 2 d = \sum_{i = 1}^{n} A_{i} B + \sum_{i = 1}^{n} A_{i} C > 2 \sum_{i = 1}^{n} A_{i} F, \end{matrix}

azaz

d > \sum_{i = 1}^{n} A_{i} F

. Ez ellentmond feladatunk feltételeinek, tehát kezdeti feltevésünk hibás volt.
Az

A_{1}

A_{2}

...

A_{n}

pontok tehát valóban egy egyenesen vannak.

Megjegyzés. Könnyen látható, hogy egy egyenesen lévő

A_{1}

A_{2}

...

A_{n}

pontok esetén, ha

n

páros, léteznek a feladat feltételeinek eleget tevő különböző

B

és

C

pontok.

Koch Dénes (Linz, Akademische Gymnasium, 10. o.t.) dolgozata alapján