| Feladat: | F.3248 | Korcsoport: 14-15 | Nehézségi fok: átlagos |
| Megoldó(k): | Boros M. Mátyás , Csirmaz Előd , Csiszár Gábor , Csóka Endre , Dancsó Zsuzsanna , Dénes Attila , Devecsery András , Fehér Lajos Károly , Gelencsér Gábor , Gerencsér Balázs , Győri Nikolett , Gyürki István , Györey Bernadett , Harangi Viktor , Horváth Gábor , Horváth György , Keszegh Balázs , Kiss Gergely , Kunszenti-Kovács Dávid , Lábó Eszter , Lábó Melinda , Máthé András , Naszódi Gergely , Pálvölgyi Dömötör , Pap Júlia , Papp Dávid , Pozsonyi Gergő , Szabadka Zoltán , Szabó Péter , Szécsi Vajk , Taraza Busra , Terpai Tamás , Tran Thanh Long , Vágvölgyi Péter , Zábrádi Gergely | ||
| Füzet: | 1999/október, 411 - 412. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Gráfelmélet, Skatulyaelv, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1998/október: F.3248 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Először megmutatjuk, hogy 5 fiú és 5 lány esetén az ismeretségek száma legfeljebb 12. Tegyük fel, hogy ez nem igaz, a tagok közt legalább 13 ismeretség van. Ekkor a skatulya-elv alapján van 2 lány, akik együttvéve legalább 6 fiút ismernek. Ennél több fiút viszont nem is ismerhetnek, hiszen 5 fiú van, és ezek közül legfeljebb egyet ismernek mindketten. Tehát van 2 lány, akik együtt 6 ismeretséggel rendelkeznek, minden fiút ismer valamelyikük, egyet pedig mindketten. Ekkor viszont a többi lánynak fejenként legfeljebb 2 ismerőse lehet, egy a fenti lányok közül az egyik, egy pedig a másik fiúismerősei közül, különben valamelyiküknek 2 közös ismerőse lenne. Így az 5 lánynak összesen legfeljebb ismerőse van, ami ellentmond a feltevésünknek.
2. Feladatunk tulajdonképpen egy gráfelméleti szélsőérték-probléma két speciális esetével foglalkozik. A probléma a következő: Legfeljebb hány éle lehet egy olyan páros gráfnak, amelynek mind csúcshalmazában csúcs van, és nem tartalmaz négyszöget? A feladat megoldása megtalálható pl. Reiman István: A geometria és határterületei című könyvének 334‐336. oldalain. Általában igaz, hogy az élek száma legfeljebb , s ez a korlát csak akkor érhető el, ha létezik ún. -adrendű véges projektív sík, ahol . 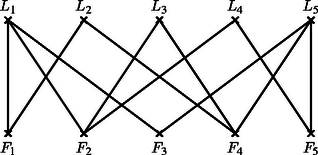 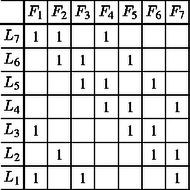 |