Kezdőlap


Feladat:	F.3247	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Terpai Tamás
Füzet:	1999/október, 410 - 411. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai bizonyítások, Négyszögek geometriája, Síkgeometriai számítások trigonometriával, Feladat
Hivatkozás(ok):	Feladatok: 1998/október: F.3247

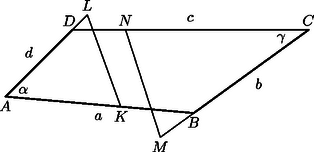
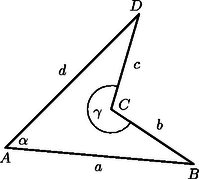
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük az $A B C D$ négyszög oldalait az ábrákon látható módon $a$ , $b$ , $c$ , $d$ -vel, az $A$ és a $C$ csúcsnál lévő szögét pedig $α$ -val, illetve $γ$ -val.
A $K L = M N$ feltétel pontosan akkor teljesül, ha $K L^{2} - M N^{2} = 0$ , vagyis ‐ a koszinusztételt alkalmazva az $A K L$ és a $C N M$ háromszögekre ‐ ha

\begin{matrix} \begin{matrix} (1) [{(\sqrt[]{a d})}^{2} + {(\sqrt[]{a d})}^{2} - 2 \sqrt[]{a d} \cdot \sqrt[]{a d} cos α] - [{(\sqrt[]{b c})}^{2} + {(\sqrt[]{b c})}^{2} - 2 \sqrt[]{b c} \cdot \sqrt[]{b c} cos γ] = 0. \end{matrix} \end{matrix}

Viszont az

A B D

és a

C B D

háromszögek közös

B D

oldalára felírt koszinusztétel szerint

\begin{matrix} B D^{2} = a^{2} + d^{2} - 2 a d cos α = b^{2} + c^{2} - 2 b c cos γ, \end{matrix}

ezért az (1) feltételt átalakíthatjuk a következő módon:

\begin{matrix} \begin{matrix} 0 & = (2 a d - 2 a d cos α) - (2 b c - 2 b c cos γ) = 2 a d - 2 b c + b^{2} + c^{2} - (a^{2} + d^{2}) = \\ = {(b - c)}^{2} - {(a - d)}^{2} = (a + b - c - d) (b + d - a - c) . \end{matrix} \end{matrix}

Mivel ekvivalens átalakításokat végeztünk, mondhatjuk, hogy

K L = M N

pontosan akkor teljesül, ha

a + b = c + d

vagy

a + c = b + d

. (Ez a feltétel úgy is fogalmazható, hogy az

A

és

C

pontok ugyanazon a

B

és

D

fókuszú hiperbolán vannak.)

Terpai Tamás (Fazekas M. Főv. Gyak. Gimn., 12. o.t.) dolgozata alapján