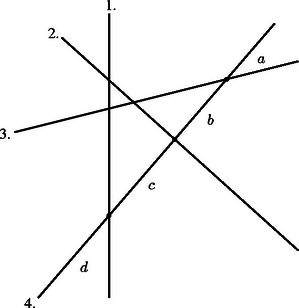
Vizsgáljuk meg először, hogy $n$ egyenes maximálisan hány részre osztja fel a síkot. Az ábra első két egyenesével $2+2$ tartomány keletkezik. Könnyen látható, hogy minden további egyenes akkor hozza létre a legtöbb új síkrészt, ha a már korábban felvett egyenesek egyikével sem párhuzamos, és nem megy át két megelőzően felvett egyenes metszéspontján. Ennek megfelelően pl. a negyedik egyenes az első három mindegyikét más-más pontban metszi, és a három ,,új'' metszéspont ezt az egyenest az $a$, $b$, $c$, $d$ szakaszokra bontja. A négy intervallumnak megfelelően négy ,,új'' síkrész jön létre. Ugyanígy beláthatjuk, hogy az $n$-edik egyenest fölvéve legfeljebb $n$ ,,új'' síkrész keletkezik. Ezért $n$ egyenes legfeljebb $N=2+2+3+\text{...}+n$ részre osztja a síkot.
Ismeretes, hogy $1+2+3+\text{...}+n=\frac{n\left(n+1\right)}{2}$, így