Kezdőlap


Feladat:	C.527	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Führer Lívia , Gajdos Béla
Füzet:	1999/október, 399 - 401. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai számítások trigonometria nélkül, Trapézok, Esetvizsgálat, Két pont távolsága, szakasz hosszúsága, C gyakorlat
Hivatkozás(ok):	Feladatok: 1999/január: C.527

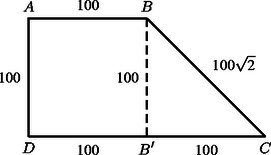
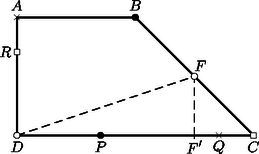
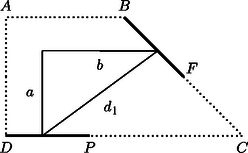
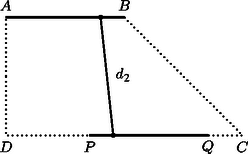
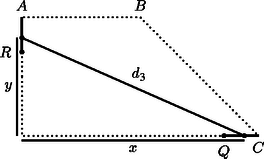
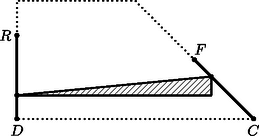
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az $A B C D$ derékszögű trapézban $B$ vetülete a $D C$ -re legyen $B'$ (1. ábra). Az $A B = D B'$ miatt $B' C = 100$ , és a $B' B C$ egyenlő szárú háromszögből $B B' = B' C = A D = 100$ , $B C = 100 \sqrt[]{2}$ .
A trapéz tehát egy 100 m oldalú négyzet és egy hozzáillesztett egyenlő szárú derékszögű háromszög, kerülete pedig: $400 + 100 \sqrt[]{2}$ .
A két őr a körüljárás irányában egyenlő távolságot tart egymással, vagyis a kerület mentén mért távolságuk a teljes kerület fele: $d = 200 + 50 \sqrt[]{2}$ .
Mivel ez a távolság a mozgás során állandó, elegendő az egyik őr mozgását vizsgálni egy félkerületnyi részen. Legyen $F$ a $B C$ szakasz felezőpontja. Amikor az egyik őr $F$ -ben van, akkor a másik éppen $D$ -ben, hiszen $D A + A B + B F = 100 + 100 + 50 \sqrt[]{2} = 200 + 50 \sqrt[]{2} = d$ .
Azt vizsgáljuk tehát, hogy mikor van a két őr légvonalban a legmesszebb egymástól, miközben az első őr $D$ -ből $F$ -be jut. A távolságok helyett keressük a távolságok négyzetének maximumát. Ezt megtehetjük, mivel a távolság mindig pozitív.
Osszuk fel a $C D$ oldalt úgy, hogy $D P = 50 \sqrt[]{2}$ , $D Q = 50 \sqrt[]{2} + 100$ , és legyen $R$ az $A D$ szakasz azon pontja, amelyre $D R = 50 \sqrt[]{2}$ (2. ábra).
Könnyen belátható, hogy (minden esetben a trapéz kerületén haladva ugyanolyan irányban) $A Q = B P = D F = R C = 200 + 50 \sqrt[]{2}$ . Kövessük az első őr útját, amíg a $D$ pontból indulva a $P$ , $Q$ , $C$ pontokon keresztül eljut az ,,átellenes'' $F$ pontba.
1. Ha az első őr $D$ -ben van, akkor a másik $F$ -ben. Ekkor a légvonalbeli távolságuk négyzete a $D F F'$ derékszögű háromszögből ( $F'$ az $F$ vetülete $D C$ -re):

\begin{matrix} D F^{2} = 50^{2} + 150^{2} = 25 000 (D F \approx 158,1) . \end{matrix}

2. Az első őr haladjon a

D P

szakaszon

P

-ig. Ekkor a második az

F B

szakaszon mozog

B

-ig; amikor

B

-be ért, a két őr távolságának négyzete:

\begin{matrix} P B^{2} = 100^{2} + {(100 - 50 \sqrt[]{2})}^{2} \approx 24 858. \end{matrix}

A közbülső helyeken (3. ábra) egy olyan derékszögű háromszög átfogójának négyzetét kapjuk, amelyben az

a

b

befogókra

a \leq 100

és

b \leq 50 \sqrt[]{2} + 100

, ezért

\begin{matrix} d_{1}^{2} \leq 100^{2} + {(50 \sqrt[]{2} + 100)}^{2} \approx 39 142. \end{matrix}

3. Haladjon az első őr tovább a

Q

pontig. Amikor az első őr

Q

-ban, akkor a második őr az

A

pontban lesz, és a távolságuk négyzete:

\begin{matrix} Q A^{2} = 100^{2} + {(100 + 50 \sqrt[]{2})}^{2} \approx 39 142. \end{matrix}

A közbülső helyeken:

a = 100

b \leq D Q = 100 + 50 \sqrt[]{2}

miatt

\begin{matrix} d_{2}^{2} < Q A^{2} = 39 142. (4. ábra) . \end{matrix}

4. Az első őr a

Q C

szakaszon mozog, a második az

A R

-en. Láttuk, hogy

C

és

R

,,átellenes'' pontok, így a két őr egyszerre érkezik

C

-be, illetve

R

-be. Azt állítjuk, hogy

Q C

, illetve a megfelelő

A R

szakaszokon mozogva az őrök távolsága növekszik (5. ábra). Ekkor ugyanis ez a távolság egy olyan derékszögű háromszög átfogója, ahol a befogók összege,

x + y

állandó, a kerülete fele.
Az

x^{2} + y^{2} = \frac{{(x + y)}^{2} + {(x - y)}^{2}}{2}

azonosságból pedig következik, hogy ekkor az átfogó hossza a befogók eltérésével nő. Mivel

Q

-ból

C

-be, illetve

A

-ból

R

-be haladva ez az eltérés valóban növekszik ‐ a hosszabbik befogó nő, a rövidebbik csökken ‐

\begin{matrix} d_{3} < R C^{2} = R D^{2} + D C^{2} = 45 000. \end{matrix}

5. Végül, ha az első őr a

C F

szakaszon halad, a második pedig az

R D

-n, akkor távolságuk kisebb, mint

R C

, hiszen a satírozott derékszögű háromszög befogói csökkennek

R D

-hez, illetve

D C

-hez képest (6. ábra).
A fentiekből látható, hogy az őrök távolsága légvonalban akkor a legnagyobb, ha egyikük a

C

, másikuk pedig az

R

pontban van. Ez a távolság

C R = \sqrt[]{45 000} \approx 222,1

méter.

Gajdos Béla (Beregszász, Bethlen G. Gimn., 11. o.t.) dolgozata alapján