|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Tekintsünk egy elemű ponthalmazt, amely megfelel a feladatban szereplő feltételeknek. Tegyük fel, hogy konvex burkának csúcsa van. Ezt a konvex -szöget egy csúcsából kiinduló átlói segítségével háromszögre bonthatjuk, amelyek mindegyikében -nak pontosan egy pontja helyezkedik el, a második feltétel értelmében. Egy ilyen háromszög határára ‐ az első feltétel miatt ‐ -nak nem eshet más pontja, mint a szóban forgó háromszög 3 csúcsa. A halmaz tehát pontosan a konvex burkának a csúcspontjaiból és az előbb említett pontból áll. Ennek következtében , azaz páros szám.
A következőkben megmutatjuk, hogy minden 3-nál nagyobb páros szám esetén megadható a síkon pont a követelményeknek megfelelően. Legyen , ekkor . Tekintsünk egy tetszőleges konvex -szöget. Ennek a belsejében vegyünk fel további pontot a következőképpen. Minden esetén legyen a és háromszögek közös részének tetszőleges belső pontja. Azt állítjuk, hogy a ponthalmaz megfelel a feltételeknek.
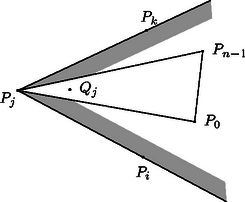
Legyen . Azt állítjuk, hogy a háromszög belseje pontjai közül egyedül a pontot tartalmazza. Először azt mutatjuk meg, hogy valóban a háromszög belső pontja. A szögtartomány tartalmazza a , , pontokat, és így a háromszög minden pontját is. Minthogy ennek a háromszögnek belső pontja, a szögtartomány belsejében van (1. ábra).
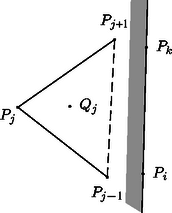
Hasonlóképpen látható, hogy a egyenesre támaszkodó, -t tartalmazó félsík belsejében található, hiszen ez a félsík tartalmazza a , , pontokat, és a háromszög belső pontja (2. ábra).
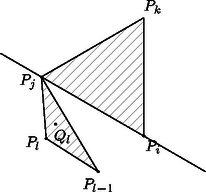
A pont tehát az 1. ábrán látható nyílt szögtartomány és a 2. ábrán látható nyílt félsík közös részében van, ez pedig éppen a háromszög belső pontjainak halmaza. Most megmutatjuk, hogy ez a halmaz pontjai közül a -n kívül egyetlen pontot sem tartalmaz. A sokszög konvex, ezért egyik csúcsa sem eshet a háromszög belsejébe. Tekintsük most valamelyik pontot, ahol . Ez a pont a háromszög belsejében helyezkedik el. Ha , akkor a egyenes elválasztja ezt a háromszöget a háromszögtől, tehát valóban nem eshet az utóbbi háromszög belsejébe. Az , , illetve esetekben a megfelelő elválasztó egyenesek rendre a , és egyenesek. A 3. ábra az esetet szemlélteti. Ezzel állításunkat bizonyítottuk.
Hátravan még annak igazolása, hogy pontjai közül semelyik három nem esik egy egyenesre. A konstrukcióból azonnal következik, hogy semelyik egyenes nem illeszkedhet -nak egyetlen további pontjára sem. Ha tehát egy egyenes pontjai közül hármat is tartalmazna, akkor tartalmaznia kellene legalább két típusú pontot. Legyenek ezek és . A egyenes a sokszög kerületét két pontban metszi, jelöljük ezeket -val és -vel. Ha ezek közül az egyik, mondjuk a sokszög csúcsa volna, akkor szükségképpen a sokszög valamely oldalának belső pontja lenne. Ekkor a háromszög a és a pontokat is tartalmazná, fenti állításunkkal ellentétben. Ha pedig és rendre a sokszög és oldalainak lenne belső pontja (feltehető, hogy , , és ilyen sorrendben, egy konvex négyszög csúcsai), akkor -nak összes pontja, amely a egyenesre illeszkedik, a négyszög belsejébe esne. Ez azonban lehetetlen, hiszen a fenti állításból könnyen levezethető, hogy ez a négyszög -nak pontosan két pontját tartalmazza.
Ezzel a feladat megoldását befejeztük.
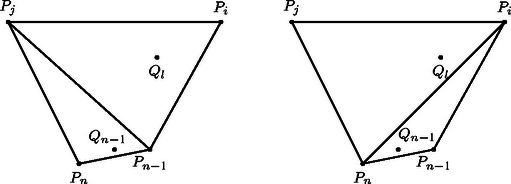
Megjegyzések. 1. Páros esetén a keresett ponthalmaz létezésére indukciós bizonyítás is adható, amelyet csak vázolunk. Tegyük fel, hogy a konvex sokszöget, és annak , , belső pontjait már meghatároztuk úgy, hogy semelyik 3 pont nem esik egy egyenesre, és minden háromszög belsejébe pontosan egy pont esik. Vegyük fel a pontot úgy, hogy konvex -szög legyen, semelyik háromszög ne tartalmazzon egyetlen pontot sem, továbbá ne legyen rajta egyik olyan egyenesen sem, amely az eddigi pontok közül kettőre már illeszkedik. ,,Látszik'', hogy ezt mindig megtehetjük. A szabatos bizonyítás megfogalmazása azonban egyáltalán nem magától értetődő. Ezek után vegyük fel a pontot a () háromszögek közös részeinek belsejében, ami éppen a és háromszögek közös részének belseje. Eközben vigyázunk arra, hogy ne essék egyetlen olyan egyenesre sem, amelyeket az eddigi pontok meghatároznak. A keletkező ponthalmaz konvex burka éppen a sokszög, és semelyik 3 pontja nem esik egy egyenesre. Az indukciós feltevésből adódik, hogy a belsejébe pontosan egy pont esik, ha . A pont konstrukciója alapján ugyanez elmondható a háromszögekről is. Végül tekintsük bármelyik háromszöget, ahol . A négyszögbe, melyet annak átlója a és a háromszögekre bont, az előzőek alapján pontosan 2 pont esik. Ezek egyike a pont, amely a háromszög egyetlen belső pontja a tekintett pontok közül. Ezért a másik pont szükségképpen a háromszögbe esik, és oda más pont nem is eshet (4. ábra).
2. Ha az esetén felrajzolható, lényegében egyértelmű konstrukcióból kiindulunk, és arra a fenti indukció lépéseit alkalmazzuk, akkor az első megoldásban ismertetett konstrukcióhoz hasonló pontrendszerhez jutunk. Felmerülhet az a gondolat, hogy lehetséges-e ,,geometriailag más szerkezetű'' ponthalmazokat is mutatni, amelyek a feltételeknek szintén megfelelnek. Ilyen ponthalmazokat is képezhetnénk az indukciós eljárás segítségével, ha nem ragaszkodunk ahhoz, hogy a , , , csúcspontokkal rendelkező konvex sokszög csúcsai éppen ilyen sorrendben kövessék egymást.
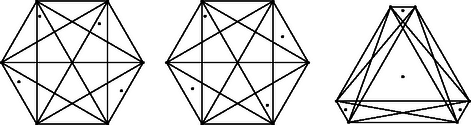
Az 5. ábrán három különböző konstrukciót mutatunk () esetén.
|
 PDF |
PDF |  MathML
MathML