Kezdőlap


Feladat:	F.3257	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Máthé András , Szabó Péter
Füzet:	1999/május, 288 - 289. oldal		PDF \| MathML
Témakör(ök):	Koordináta-geometria, Harmadfokú függvények, Függvényvizsgálat, Síkgeometriai számítások trigonometria nélkül, Számtani-mértani egyenlőtlenségek, Körök, Feladat
Hivatkozás(ok):	Feladatok: 1998/december: F.3257

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Induljunk ki az $x^{2}$ , $1 - x^{2}$ számokra felírt számtani és mértani közepek között fennálló egyenlőtlenségből ( $x^{2} \geq 0$ , $1 - x^{2} \geq 0$ ):

\begin{matrix} \frac{1}{2} = \frac{x^{2} + (1 - x^{2})}{2} \geq \sqrt[]{x^{2} (1 - x^{2})} = | x | \sqrt[]{1 - x^{2}}, \end{matrix}

ezért

\begin{matrix} \sqrt[]{1 - x^{2}} \geq 2 | x | (1 - x^{2}) = 2 | x (1 - x^{2}) | = | f (x) | . \end{matrix}

(1)

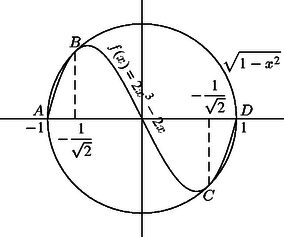
(1) éppen azt jelenti, hogy a vizsgált

[- 1, 1]

intervallumon

f (x)

görbéjét tartalmazza az origó körüli 1 egység sugarú kör. Mivel egy zárt körlap két pontjának a távolsága legfeljebb annyi, mint a kör átmérője, ezért az

f

görbéjén lévő bármely két pont távolsága legfeljebb 2. Ez elérhető, például az

A = (- 1; 0)

és

D = (1; 0)

pontok esetén.
Ahhoz, hogy ezt a határt valóban elérjük, mindkét pontnak a köríven kell lennie, mégpedig egymással átellenesen. Az előbb említettől különböző megoldást úgy kaphatunk, ha

x \neq \pm 1

(és

\sqrt[]{1 - x^{2}} \neq 0

).
(1)-ben viszont pontosan akkor áll egyenlőség, ha a számtani‐mértani közép közötti egyenlőtlenségben is egyenlőség van, azaz

x^{2} = 1 - x^{2}

, tehát

x = \pm \frac{1}{\sqrt[]{2}}

. Ez két pontot ad:

B = (- \frac{1}{\sqrt[]{2}}; \frac{1}{\sqrt[]{2}})

és

C = (\frac{1}{\sqrt[]{2}}; - \frac{1}{\sqrt[]{2}})

. Ezek valóban a körön helyezkednek el egymással szemben és

f

görbéjén is rajta vannak. Így két megoldást kaptunk: az

A

D

és a

B

C

pontpárokat.

Szabó Péter (Fazekas M. Főv. Gyak. Gimn., 12. o.t.) dolgozata alapján