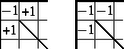
Nem lehet minden kiindulási állapothoz véges sok lépésben visszajutni. A megoldók több különböző ellenpéldát találtak, egy ilyet mutat az 1. ábra. Ebben a táblázatban a sarkokban álló $\left(-1\right)$-esek két-két élszomszédja $+1$; az oldalak mentén mindegyik elemre igaz, hogy vagy mind a három élszomszédja $+1$, vagy közülük pontosan kettő $\left(-1\right)$; végül a belső, négy élszomszéddal rendelkező mezők vagy csupa $\left(+1\right)$-gyel, vagy két $\left(-1\right)$ és két $\left(+1\right)$-gyel szomszédosak.
Az első lépés után tehát a táblázat összes eleme $\left(+1\right)$ lesz, ezután pedig a táblázat nem változik.
Nemcsak $9\times 9$-es, de más méretek (legalább $2\times 2$-es tábla) esetén sem igaz az állítás. Mindig van ugyanis olyan kiindulás, amely nem állhat vissza: legyen például a bal felső elem $\left(-1\right)$, és a táblázat legyen a főátlóra szimmetrikus (2. ábra). Ekkor az első lépés után a bal felső elem $\left(+1\right)$-re változik, és a további lépések után is az marad, hiszen két szomszédja a szimmetria miatt egyszerre változik. Így ebben a mezőben soha nem lesz újra $-1$, a táblázat tehát soha nem lesz azonos a kezdetivel.