Feladat:	Gy.3229	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Ambrus Gergely ,  Andrássy Zoltán ,  Baharev Ali ,  Bárány Zsófi ,  Deli Lajos ,  Erdei Zsuzsa ,  Fazekas Éva ,  Fekete Árpád ,  Gerencsér Balázs ,  Germán Tibor ,  Horváth Balázs ,  Horváth László ,  Kiss Gergely ,  Kunszenti-Kovács Dávid ,  Lábó Eszter ,  Leipold Diána ,  Pallos Péter ,  Pesti Gábor ,  Pogátsa Attila ,  Szalay Zsófia ,  Szebenyi Zoltán ,  Tóth Ágnes ,  Varjú Péter ,  Venter György ,  Zábrádi Gergely ,  Zsidó Csilla Laura
Füzet:	1999/április, 223 - 224. oldal		PDF  |  MathML
Témakör(ök):	Tetraéderek, Szabályos testek, Térgeometriai bizonyítások, Gyakorlat
Hivatkozás(ok):	Feladatok: 1998/október: Gy.3229

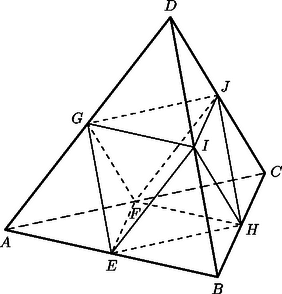
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Tekintsünk egy 2 egység élű $ABCD$ szabályos tetraédert. Legyen az élek felezőpontja $E$, $F$, $G$, $H$, $I$, $J$ (1. ábra). Az $AEFG$ tetraéder például az $ABCD$-nek $A$ pontból történő $1:2$ arányú kicsinyítése, ezért szabályos, és élei egységnyiek. Hasonlóan kaphatók a $B$, $C$ és $D$ csúcsú kicsinyített tetraéderek. Könnyen belátható, hogy $EFGHIJ$ egy egységnyi élű szabályos oktaéder. Élei ugyanis mind egységnyiek, mind a 8 lapja szabályos háromszög, tehát élszögei egyenlők és lapszögei is egyenlők, mert mindegyikük a szabályos tetraéder lapszögének kiegészítő szöge. Így a 2 egység élű szabályos tetraédert 4 szabályos tetraéderre és egy szabályos oktaéderre daraboltuk fel. Megfordítva, az is igaz, hogy 4 egybevágó szabályos tetraéderből és egy velük egyező élű szabályos oktaéderből egy kétszer akkora élű szabályos tetraéder rakható össze. A Gy. 3221. (KöMaL 1999/3. szám, 151. oldal) gyakorlatban bebizonyítottuk, hogy 6 egybevágó szabályos oktaéderből és 8 velük egyező élű szabályos tetraéderből össze lehet rakni egy kétszer akkora élű szabályos oktaédert. Ezután a feladat állítását a következőképpen igazolhatjuk. Rakjunk össze szabályos tetraéderekből és oktaéderekből kétszer akkora élű tetraédereket és oktaédereket. Ezt folytatva négyszer, nyolcszor, $\text{...}$ akkora élű, tehát tetszőlegesen nagy élű szabályos oktaéder építhető.  Horváth László (Csurgó, Nagyváthy Középiskola, 11. o.t.) és    Varjú Péter Szeged, Radnóti M. Gimn., 10. 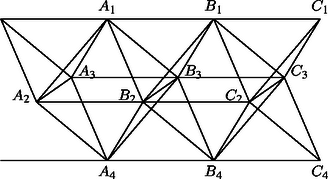o.t.) dolgozata alapján   II. megoldás. Illesszünk össze két szabályos oktaédert úgy, hogy egyik élük közös, és a 2. ábrán $A_1$-gyel, illetve $B_1$-gyel jelölt csúcsok távolsága éppen az élhossz legyen. Az elhelyezés révén $A_1{A}_2\Vert B_1{B}_2\Vert C_1{C}_2$, ezért az $A_1{A}_2{B}_2$ háromszög és a $B_1{B}_2{C}_2$ háromszög egy síkban van. Ugyanebben a síkban van az $A_1{B}_1{B}_2$ háromszög is. Hasonló mondható az $A_1{B}_1{B}_3$ háromszögről, ez az $A_1{A}_3{B}_3$ és a $B_1{B}_3{C}_3$ háromszögekkel van egy síkban. Ebből következik, hogy az $A_1{B}_1{B}_2{B}_3$ tetraéder szabályos, és illeszkedik két szabályos oktaéderhez. Hasonlóan helyezkedik el a két oktaéder között az $A_4{B}_2{B}_3{B}_4$ szabályos tetraéder. Így az oktaéderek közötti ,,résekbe'' szabályos tetraédereket illeszthetünk, amit vég nélkül folytatva egy végtelen hasáb jön létre. A hasábot egy, az $A_1{B}_1$-re merőleges sík rombuszban metszi. Mivel a metsző sík hézag és átfedés nélkül lefedhető ilyen rombuszokkal, a tér is kitölthető hézag és átfedés nélkül a szóban forgó végtelen hasábokkal.  Ambrus Gergely (Szeged, Radnóti M. Gimn., 10. o.t.) és    Venter György (Fazekas M. Főv. Gyak. Gimn., 11. o.t.) dolgozata alapján