Kezdőlap


Feladat:	Gy.3205	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Gyenes Zoltán , Kunszenti-Kovács Dávid , Legány Csaba , Papp Dávid
Füzet:	1999/március, 146 - 147. oldal		PDF \| MathML
Témakör(ök):	Gúlák, Háromszögek geometriája, Síkgeometriai szerkesztések, Gyakorlat
Hivatkozás(ok):	Feladatok: 1998/április: Gy.3205

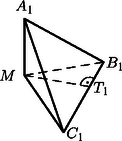
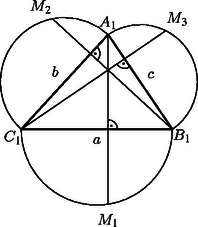
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyenek az $A B C$ háromszög oldalai $a$ , $b$ és $c$ . Tekintsünk egy olyan gúlát (1. ábra), amelynek $M$ csúcsából kiinduló élei páronként merőlegesek, és az élek hossza rendre

\begin{matrix} \begin{matrix} M C_{1} = \sqrt[]{\frac{a^{2} + b^{2} - c^{2}}{2}}, M B_{1} = \sqrt[]{\frac{a^{2} + c^{2} - b^{2}}{2}}, \\ M A_{1} = \sqrt[]{\frac{b^{2} + c^{2} - a^{2}}{2}} . \end{matrix} \end{matrix}

Ilyen gúla nyilván létezik, hiszen az

A B C

háromszög hegyesszögű. Azt fogjuk bizonyítani, hogy ennek a gúlának a hálózata egybevágó a feladatbeli hatszöggel.
Számítsuk ki először az

A_{1} B_{1} C_{1}

háromszög oldalait. A Pithagorasz-tétel szerint

\begin{matrix} \begin{matrix} B_{1} C_{1} = \sqrt[]{\frac{a^{2} + b^{2} - c^{2}}{2} + \frac{a^{2} + c^{2} - b^{2}}{2}} = \sqrt[]{a^{2}} = a . \end{matrix} \end{matrix}

Hasonlóan kapjuk, hogy a másik két oldal

b

, illetve

c

. Az

A_{1} B_{1} C_{1}

háromszög tehát egybevágó az

A B C

háromszöggel.
Húzzunk most merőlegest

M

-ből a

B_{1} C_{1}

-re, legyen ennek talppontja

T_{1}

. Mivel

M A_{1}

merőleges

M B_{1}

és

M C_{1}

-re, merőleges az

M B_{1} C_{1}

háromszög síkjára, tehát

B_{1} C_{1}

-re is. Így

B_{1} C_{1}

merőleges lesz az

A_{1} M T_{1}

háromszög síkjára, amiből következik, hogy

A_{1} T_{1} ⊥ B_{1} C_{1}

. Ezért, ha az

M B_{1} C_{1}

lapot az

a

oldal körül az

A_{1} B_{1} C_{1}

háromszög síkjába forgatjuk,

M

képe ‐ ami a 2. ábrán

M_{1}

‐ éppen az

A_{1} B_{1} C_{1}

háromszög

A_{1}

-ből húzott magasságvonalának és és a

B_{1} C_{1}

oldal Thalesz-körének (egyik) metszéspontja lesz. Hasonló igaz az

M_{2}

és

M_{3}

pontokra.
A leírtakból következik, hogy a 2. ábrán

A_{1} M_{3} B_{1} M_{1} C_{1} M_{2}

az első ábra gúlájának hálózata.

Gyenes Zoltán (Budapest, Apáczai Cs. J. Gimn., 10. o.t.)