Kezdőlap


Feladat:	N.179	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Gerbicz Róbert , Gyenes Zoltán , Juhász András , Lukács László , Terpai Tamás , Végh A. László
Füzet:	1999/február, 96 - 98. oldal		PDF \| MathML
Témakör(ök):	Koszinusztétel alkalmazása, Síkgeometriai bizonyítások, Alakzatok köré írt kör, Háromszög-egyenlőtlenség alkalmazásai, Nehéz feladat
Hivatkozás(ok):	Feladatok: 1998/szeptember: N.179

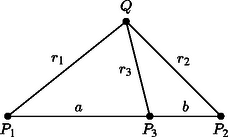
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen a három pont $P_{1}$ , $P_{2}$ és $P_{3}$ . Ha valamelyik kettő egybeesik, akkor ezek köré ugyanakkora sugarú köröket rajzolva elérhetjük, hogy legyen $2 n^{2}$ olyan pont, amelyen három kör is átmegy. A továbbiakban ezért feltesszük, hogy $P_{1}$ , $P_{2}$ és $P_{3}$ különbözőek, valamint $P_{3}$ a $P_{1} P_{2}$ szakasz belsejében helyezkedik el.
Legyen $a = P_{1} P_{3}$ és $b = P_{3} P_{2}$ , és vizsgáljuk meg, hogy $P_{1}$ , $P_{2}$ , $P_{3}$ köré egy $r_{1}$ , $r_{2}$ , illetve $r_{3}$ sugarú kört rajzolva, a három kör mikor megy át egy ponton. Legyen a $P_{i}$ körüli $r_{1}$ sugarú és a $P_{2}$ körüli $r_{2}$ sugarú kör metszéspontja $Q$ . Ahhoz, hogy ez a metszéspont létrejöjjön, szükséges és elégséges, hogy teljesüljenek a háromszög-egyenlőtlenségek az $r_{1}$ , $r_{2}$ és $a + b$ számokra.
Tegyük fel, hogy a $P_{3}$ körüli, $r_{3}$ sugarú kör is átmegy $Q$ -n. Felírva a koszinusztételt a $P_{1} P_{3} Q$ és $P_{2} P_{3} Q$ háromszögekre,

\begin{matrix} cos P_{1} P_{3} Q ∢ = \frac{a^{2} + r_{3}^{2} - r_{1}^{2}}{2 a r_{3}} = - cos P_{2} P_{3} Q ∢ = - \frac{b^{2} + r_{3}^{2} - r_{2}^{2}}{2 b r_{3}}, \end{matrix}

ami rendezve a

\begin{matrix} b (r_{1}^{2} - a^{2}) + a (r_{2}^{2} - b^{2}) = (a + b) r_{3}^{2} \end{matrix}

(1)

alakba írható.
Legyen

d = {min}_{}^{} (\frac{a}{n}, \frac{b}{n})

. Rajzoljuk meg

P_{1}

körül az

\begin{matrix} r_{11} = \sqrt[]{a^{2} + a d}, r_{12} = \sqrt[]{a^{2} + 2 a d}, ..., r_{1 n} = \sqrt[]{a^{2} + n a d} \end{matrix}

sugarú köröket,

P_{2}

körül az

\begin{matrix} r_{21} = \sqrt[]{b^{2} + b d}, r_{22} = \sqrt[]{b^{2} + 2 b d}, ..., r_{2 n} = \sqrt[]{b^{2} + n b d} \end{matrix}

sugarú köröket,

P_{3}

körül pedig az

\begin{matrix} r_{31} = \sqrt[]{2 \frac{a b d}{a + b}}, r_{32} = \sqrt[]{3 \frac{a b d}{a + b}}, ..., r_{3 n} = \sqrt[]{(n + 1) \frac{a b d}{a + b}} \end{matrix}

sugarú köröket. Ezzel a választással

b (r_{1}^{2} - a^{2})

és

a (r_{2}^{2} - b^{2})

a b d

2 a b d

...

n a b d

számokon,

(a + b) r_{3}^{2}

pedig a

2 a b d

3 a b d

...

(n + 1) a b d

számokon fut végig.
Az

r_{1 j}

r_{2 j}

és

a + b

számokra mindig teljesülnek a megfelelő háromszög-egyenlőtlenségek, mert

\begin{matrix} \begin{matrix} a < r_{1 j} \leq \sqrt[]{a^{2} + n a d} \leq \sqrt[]{a^{2} + a b} < a + b \\ és \\ b < r_{2 j} \leq \sqrt[]{b^{2} + n b d} \leq \sqrt[]{b^{2} + a b} < a + b . \end{matrix} \end{matrix}

Az egy ponton átmenő körhármasoknak a száma tehát megegyezik az

x + y = z

egyenlet azon megoldásainak számával, amelyekben

x

y \in {1, 2, ..., n}

és

z \in {2, 3, ..., n + 1}

. Az ilyen számhármasok száma

\begin{matrix} \sum_{x = 1}^{n} (n + 1 - x) = \frac{n (n + 1)}{2} > \frac{n^{2}}{2} . \end{matrix}

Mivel minden ilyen számhármashoz két metszéspont tartozik, összesen több, mint

n^{2}

olyan pont van, amelyen három kör megy át. A feladat állítása tehát igaz a

c = 1

választással.

Megjegyzés. Az előbbi konstrukciót módosítva, az

\begin{matrix} r_{3 i} = \sqrt[]{(⌈ \frac{n}{2} ⌉ + i) \frac{a b d}{a + b}} (i = 1, 2, ..., n) \end{matrix}

választással azoknak a pontoknak a száma, amelyeken három kör megy át,

\frac{3}{2} n^{2}

lesz ha

n

páros, és

\frac{3 n^{2} + 1}{2}

n

paratlan. Azt is be lehet bizonyítani, hogy ennél több már nem érhető el. A legnagyobb

c

érték tehát, amivel az állítás igaz, a

\frac{3}{2}

Terpai Tamás (Fazekas M. Főv. Gyak. Gimn., 12. o.) dolgozata alapján