Kezdőlap


Feladat:	F.3237	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Székelyhidi Gábor
Füzet:	1999/január, 38 - 39. oldal		PDF \| MathML
Témakör(ök):	Vektorok lineáris kombinációi, Paralelepipedon, Feladat
Hivatkozás(ok):	Feladatok: 1998/május: F.3237

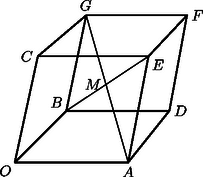
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a hasáb csúcsait az ábrán látható módon $O$ , $A$ , $B$ , $C$ , $D$ , $E$ , $F$ , $G$ -vel. Legyen $\vec{O A} = a$ , $\vec{O B} = b$ és $\vec{O C} = c$ . Ekkor $a$ , $b$ és $c$ lineárisan független vektorok. Mivel a $D$ csúcs az $O A B$ síkban van, azért vannak olyan $0$ -tól különböző $x$ , $y$ számok, amelyekre $\vec{O D} = x a + y b$ . A hasáb tulajdonságaiból következik, hogy $\vec{O E} = a + c$ , $\vec{O G} = b + c$ és $\vec{O F} = x a + y b + c$ .
Ismert, hogy ha az $O$ -ból egy $K L$ szakasz végpontjaiba mutató vektorok $k$ és $l$ , akkor a szakasz tetszőleges $N$ pontja esetén az $\vec{O N}$ vektor felírható $α k + (1 - α) l$ alakban, ahol $α$ 0 és 1 közti valós szám. Legyen a hasáb testátlóinak metszéspontja $M$ . Mivel $M$ rajta van az $A G$ átlón, azért van olyan $β$ szám, amelyre

\begin{matrix} \vec{O M} = β \cdot \vec{O A} + (1 - β) \vec{O G} = β \cdot a + (1 - β) (b + c) . \end{matrix}

(1)

M

rajta van a

B E

és az

O F

átlókon is, ezért vannak olyan

γ

és

δ

számok, amelyekre

\begin{matrix} \begin{matrix} \vec{O M} & = γ \cdot \vec{O B} + (1 - γ) \vec{O E} = (1 - γ) a + γ b + (1 - γ) c és & (2) \\ \vec{O M} & = δ \cdot \vec{O F} = δ (x a + y b + c) . & (3) \end{matrix} \end{matrix}

\vec{O M}

-et viszont egyértelműen lehet felírni a lineárisan független

a

b

és

c

vektorok kombinációjaként, azért az (1), (2) és (3) egyenletekben

a

b

, illetve

c

együtthatói rendre ugyanazok a valós számok lesznek; tehát

\begin{matrix} \begin{matrix} β & = 1 - γ = δ \cdot x, \\ 1 - β & = γ = δ \cdot y, \\ 1 - β & = 1 - γ = δ . \end{matrix} \end{matrix}

Ezen egyenletekből nyilvánvalóan következik, hogy

x = y = 1

, azaz

\vec{O D} = \vec{O A} + \vec{O B}

, ami azt jelenti, hogy a hasáb alaplapja paralelogramma, tehát a hasáb paralelepipedon.

Székelyhidi Gábor (Kuwait, New English School, 11. o.t.) dolgozata alapján