| Feladat: | Gy.3201 | Korcsoport: 14-15 | Nehézségi fok: nehéz |
| Megoldó(k): | Bárány Kristóf , Devecsery András , Fehér Lajos Károly , Gelencsér Gábor , Gyenes Zoltán , Győri Nikolett , Harangi Viktor , Juhász András , Keszegh Balázs , Kiss Gergely , Kunszenti-Kovács Dávid , Máthé András , Papp Dávid , Pesti Gábor , Szabadka Zoltán , Szabó Péter , Székelyhidi Gábor , Terpai Tamás , Tóth Ágnes , Varjú Péter , Végh A. László | ||
| Füzet: | 1999/január, 29 - 30. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Lefedések, Rekurzív sorozatok, Logikai feladatok, Gyakorlat | ||
| Hivatkozás(ok): | Feladatok: 1998/április: Gy.3201 | ||
|
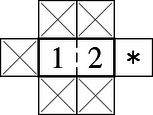
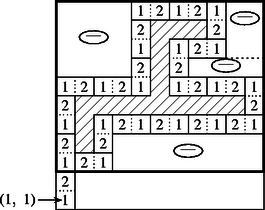
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. -es helyett általában olyan ,,sakktáblán'' bizonyítjuk az állítást, amelynek oldalai (a mezők élhosszában mérve) páratlan hosszúságúak. Vezessünk be egy a sakkjátékban használatoshoz hasonló koordinátarendszert a tábla mezőinek jelölésére; eszerint a ,,bal alsó'' mező koordinátái , az eggyel fölötte levőé stb. (1) A továbbiakban megmutatjuk, hogy ha egy olyan dominót szemelünk ki, amely a tábla egyik sarkát ‐ pl. az koordinátájút ‐ fedi le, és a saroknál lévő mezője az 1-es, akkor képezve ennek rákövetkezőjét, a rákövetkező rákövetkezőjét stb., végül az üres sarok lesz az eljárásban -gal jelölendő mező, amelynél a dominók eme sorozatának képzése szükségképpen megakad. Ha állításunkkal szemben nem ez a helyzet, akkor a láncban mindegyik dominónak van rákövetkezője, és egyszer olyan dominót kapunk rákövetkezőként, amely már korábban előfordult a sorozatban; a 2. ábra ábrázolja azt a helyzetet, amikor ez az ismétlődés először bekövetkezik. A rákövetkezési sorrendben ,,kört'' alkotó dominókból álló alakzatot foglaljuk bele abba a legkisebb téglalapba, amelynek oldalai az eredeti tábla éleivel párhuzamosak (az ábrán ez a vastag vonallal határolt téglalap). Mivel a dominók részeinek számozása összhangban van a sakktábla szokásos színezésével (pl. az 1-es mezők mindig fehérek, a 2-esek pedig feketék), azért az ábrából látható, hogy a befoglaló téglalap mindkét oldala páratlan hosszúságú, ezért a ‐ mezőkben mért ‐ területe páratlan. Ebből a területből kivonva a ─ jellel ellátott téglalapok összterületét, a dominók által közrezárt területhez jutunk. Világos, hogy a dominók páros mérőszámú területet fednek le, hiszen mindegyik dominó területe 2 egység. Látható továbbá, hogy a dominók alkotta ,,töröttvonal'' töréspontjai mindig 1-es jelű mezőben vannak, ezért a levonandó téglalapok területe páros (szemköztes csúcsaik azonos színűek). Ezzel azt kaptuk, hogy a dominókör által bekerített (az ábrán vonalkázással jelölt) rész páratlan sok mezőt tartalmaz. Így lennie kell a bekerített részen olyan mezőnek, amelyet nem fed le dominó. Ez azonban lehetetlen, mivel mindegyik belső mező le van fedve (egyedül az egyik sarok fedetlen). Az (1) állítást ezzel igazoltuk. Jelölje ezután , , , azt a dominósorozatot, amelyben 1-es mezője az sarok, rákövetkezője (, 2, , ), és -nek nem létezik rákövetkezője, azaz (az 1. ábra jelöléseivel) 2-es jelű mezőjének -gal jelölendő élmenti szomszédja a tábla egyetlen fedetlen sarokmezője. Így eltolható úgy, hogy az eredetileg által lefedett 1-es mező legyen üres. Az eljárást ezzel az üres mezővel és -gyel folytatjuk, s.í.t.; végül lesz fedetlen.
  |