Kezdőlap


Feladat:	F.3235	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Baharev Ali , Bárány Kristóf , Bíró Ádám , Csikvári András , Győri Nikolett , Harangi Viktor , Horváth Hedvig , Juhász András , Keszegh Balázs , Kunszenti-Kovács Dávid , Lippner Gábor , Lovas Róbert , Máthé András , Páles Csaba , Pogány Ádám , Pszota Anikó , Szabadka Zoltán , Szabó Péter , Székelyhidi Gábor , Taraza Busra , Terpai Tamás , Tóth Ádám , Tóth Ágnes , Zombori Tamás
Füzet:	1998/december, 541 - 543. oldal		PDF \| MathML
Témakör(ök):	Egyéb sokszögek geometriája, Terület, felszín, Paralelogrammák, Feladat
Hivatkozás(ok):	Feladatok: 1998/május: F.3235

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megmutatjuk, hogy ha $K$ és $L$ olyan $2 n$ oldalú sokszögek ( $n \geq 2$ egész), amelyek oldalfelező pontjai egybeesnek, akkor a két sokszögnek egyenlő a területe. Állításunkat $n$ szerinti teljes indukcióval bizonyítjuk.
Ha $n = 2$ , akkor $K$ és $L$ négyszögek. Tudjuk, hogy egy négyszög oldalfelező pontjai olyan paralelogrammát alkotnak, amelynek oldalai párhuzamosak a négyszög átlóival, hosszuk pedig az átlók hosszának fele. Ha tehát $K$ és $L$ oldalfelező pontjai egybeesnek, akkor $K$ és $L$ megfelelő átlói egyenlő hosszúak és párhuzamosak. Ebből viszont következik, hogy $K$ és $L$ egyenlő területűek, mert ismert, hogy ha egy négyszög átlóinak hossza $e$ és $f$ , az átlók szöge pedig $φ$ , akkor a területe

\begin{matrix} T = \frac{e \cdot f \cdot sin φ}{2} . \end{matrix}

(1)

Tegyük most fel, hogy az állítást már beláttuk

2 k

-szögekre, és legyen

K

és

L

két olyan

2 (k + 1)

-szög, amelyek oldalfelező pontjai egybeesnek. Jelöljük a sokszögek csúcsait

K_{1}

K_{2}

...

K_{2 k + 2}

, illetve

L_{1}

L_{2}

...

L_{2 k + 2}

-vel úgy, hogy a

K_{i} K_{i + 1}

és az

L_{i} L_{i + 1}

oldalak közös felezőpontja legyen

F_{i}

(

i = 1

, 2,

...

2 k + 2

). Rajzoljuk meg a sokszögekben a

K_{1} K_{4}

és az

L_{1} L_{4}

átlókat. E két átló a

K_{1} K_{2} K_{3} K_{4}

és az

L_{1} L_{2} L_{3} L_{4}

‐ esetleg hurkolt ‐ négyszögeknek egy-egy oldala. Mivel a két négyszög másik három-három oldalának felezőpontjai egybeesnek, és a négyszögek oldalfelező pontjai paralelogrammát alkotnak, amit három csúcsa egyértelműen meghatároz, ezért

K_{1} K_{4}

és

L_{1} L_{4}

felezőpontjai is egybeesnek. Vagyis a két átló a

K

és

L

(2 k + 2)

-szögeket úgy osztja egy-egy

K'

és

L'

2 k

-szögre és a

K''

, valamint

L''

négyszögekre, hogy azok oldalfelező pontjai egybeesnek. Ekkor viszont az indukciós feltevésünk szerint

K'

területe megegyezik

L'

területével,

K''

területe pedig

L''

területével. Ebből viszont következik, hogy

K

területe megegyezik

L

területével (a 2. ábrán látható esetben

L''

hurkolt négyszög, amelynek területét az (1) képlet előjelesen adja).
Ezzel beláttuk, hogy ha két páros oldalszámú sokszög oldalfelező pontjai egybeesnek, akkor a két sokszög területe egyenlő.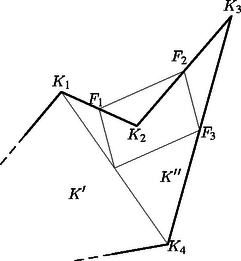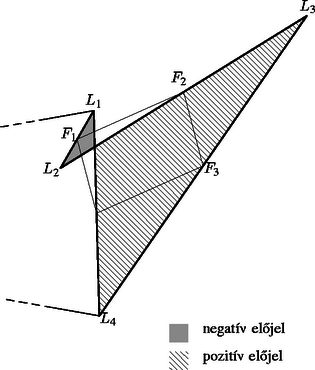

Megjegyzés. Páratlan oldalszámú sokszögek esetén több is igaz: ha két páratlan oldalszámú sokszög oldalfelező pontjai esnek egybe, akkor a két sokszög nemcsak egyenlő területű, hanem egybevágó is. Ezt az állítást is be lehet bizonyítani a megoldásunkban leírt ,,darabolós'' módszerrel.