Kezdőlap


Feladat:	Gy.3204	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Papp Dávid
Füzet:	1998/december, 532. oldal		PDF \| MathML
Témakör(ök):	Terület, felszín, Háromszögek hasonlósága, Számtani-mértani egyenlőtlenségek, Törtfüggvények, Gyakorlat
Hivatkozás(ok):	Feladatok: 1998/április: Gy.3204

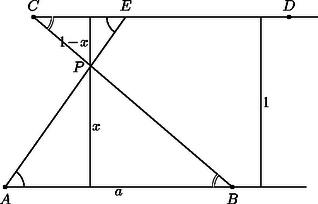
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az ábrán az $A B$ szakasz hosszát $a$ -val, $P$ és $A B$ távolságát $x$ -szel jelöltük, a két párhuzamos egyenes távolsága pedig legyen 1. Az $A B P$ és $E C P$ háromszögek szögei páronként megegyeznek, tehát ezek a háromszögek hasonlók. Ezért $C E = a \frac{1 - x}{x}$ . Így a háromszögek területeinek $T$ összege:

\begin{matrix} T = \frac{a x}{2} + \frac{a {(1 - x)}^{2}}{2 x} = \frac{a}{2} \cdot \frac{2 x^{2} - 2 x + 1}{x}, \end{matrix}

és mivel

P

belső pont,

0 < x < 1

T

pontosan akkor lesz a legkisebb, amikor a

\frac{2 x^{2} - 2 x + 1}{x}

tört a legkisebb.

\begin{matrix} \frac{2 x^{2} - 2 x + 1}{x} = 2 x + \frac{1}{x} - 2 \geq 2 \sqrt[]{2 x \cdot \frac{1}{x}} - 2 = 2 \sqrt[]{2} - 2, \end{matrix}

ahol a számtani és mértani közép közötti egyenlőtlenségből azt kaptuk, hogy a tört értéke biztosan nem kisebb a

2 \sqrt[]{2} - 2

értéknél. Az is következik, hogy ezt a minimumot meg is kapjuk, ha

0 < x < 1

: ha

2 x = \frac{1}{x}

, akkor

x = \frac{1}{\sqrt[]{2}}

. Ez a feltétel a

P

pont helyzetét egyértelműen határozza meg a

B C

szakaszon. Továbbá ‐ bár ezt a feladat nem kérdezi ‐ a

T

minimumát is megadhatjuk:

T_{{min}_{}^{}} = a (\sqrt[]{2} - 1)

Papp Dávid (Budapest, Szent István Gimn., 10. o.t.)