Feladat:	Gy.3203	Korcsoport: 14-15	Nehézségi fok: átlagos
Megoldó(k):	Csirmaz Előd ,  Siklósi Dávid
Füzet:	1998/december, 530 - 532. oldal		PDF  |  MathML
Témakör(ök):	Rombuszok, Alakzatba írt kör, Érintősokszögek, Terület, felszín, Gyakorlat
Hivatkozás(ok):	Feladatok: 1998/április: Gy.3203

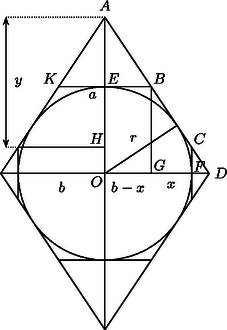
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. A nyolcszög $t$ területét úgy fogjuk kiszámítani, hogy a rombusz $T=2ab$ területéből kivonjuk az érintők által levágott négy háromszög területét. Használjuk az ábra jelöléseit. Legyen az $AEB$ háromszög területe $t_1$, a $CFD$ háromszögé $t_2$. Könnyen látható, hogy $t_1=\frac{\left(b-x\right)\left(a-r\right)}{2}$ és $t_2=\frac{\left(a-y\right)\left(b-r\right)}{2}$. A párhuzamos szelők tétele szerint $\frac{x}{r}=\frac{b}{a}$, amiből $x=\frac{br}{a}$, és ugyanígy $y=\frac{ar}{b}$. Tekintve, hogy a rombusz oldala $\sqrt[]{a^2+b^2}$, az $AOD$ háromszög kétszeres területét kétféleképpen kiszámítva: $ab=r\sqrt[]{a^2+b^2}$, tehát $r=\frac{ab}{\sqrt[]{a^2+b^2}}$. Ezekkel az értékekkel az érintők által levágott négy háromszög területének összege: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{c}\hfill {\displaystyle 4t_1+4t_2=2\left[\left(a-r\right)\left(b-\frac{br}{a}\right)+\left(b-r\right)\left(a-\frac{ar}{b}\right)\right]=}\\ \hfill {\displaystyle =2\left(2ab-2ar-2br+r^2\frac{a^2+b^2}{ab}\right)=}\end{array}}}\end{array}$ $\begin{array}{c}{\displaystyle =2\left(2ab-2\left(a+b\right)\frac{ab}{\sqrt[]{a^2+b^2}}+\frac{a^2{b}^2}{a^2+b^2}\cdot \frac{a^2+b^2}{ab}\right)=2\cdot \left(3ab-2ab\frac{a+b}{\sqrt[]{a^2+b^2}}\right)\mathrm{.}}\end{array}$ A nyolcszög területe: $\begin{array}{c}{\displaystyle t=T-\left(4t_1+4t_2\right)=2ab-2\cdot \left(3ab-2ab\frac{a+b}{\sqrt[]{a^2+b^2}}\right)=4ab\left(\frac{a+b}{\sqrt[]{a^2+b^2}}-1\right)\mathrm{.}}\end{array}$  Csirmaz Előd (Fazekas M. Főv. Gyak. Gimn., 9. o.t.)    Siklósi Dávid (Fazekas M. Főv. Gyak. Gimn., 9. o.t.)   II. megoldás. Az érintők levágta szemközti háromszögeket összetolva az eredeti rombuszhoz hasonló rombuszokat kapunk. Ismeretes, hogy hasonló alakzatok területének aránya egyenlő a hasonlóság arányának négyzetével. Ennek alapján az $AKB$ háromszögből és $OD$-re vonatkozó tükörképéből kialakuló rombusz $4t_1$ területe a következőképpen nyerhető: $\frac{4t_1}{T}={\left(\frac{a-r}{a}\right)}^2$, ahonnan $4t_1=2ab{\left(\frac{a-r}{a}\right)}^2$, ahol felhasználtuk, hogy $T=2ab$. Hasonlóan kapjuk: $4t_2=2ab{\left(\frac{b-r}{b}\right)}^2$. A nyolcszög területe: $t=2ab\left[1-{\left(\frac{a-r}{a}\right)}^2-{\left(\frac{b-r}{b}\right)}^2\right]$, amiből $r=\frac{ab}{\sqrt[]{a^2+b^2}}$ behelyettesítése után némi számolással az első megoldásban nyert eredményt kapjuk.