|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás. A háromszög területe a szokásos jelölésekkel . Mivel és , és . Ezért és . Mivel , pozitív számok, azt nyerjük, hogy és . Ezekből következik, hogy , ami csak úgy lehetséges, ha , vagyis .
Derékszögű háromszögben az egyik befogóhoz tartozó magasság a másik befogó, ezért a feltételek szerint és , ahonnan következik.
Tehát a háromszög derékszögű és egyenlő szárú, így a szögei: , , .
| Zalán Péter (Budapesti Evangélikus Gimn., 9. o.t. |
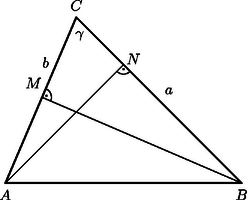
II. megoldás. Ábránkon az a két magasság, amelyekről a két feltétel szól, , illetve . A feltételek szerint és . Írjuk fel az és háromszögekre a Pitagorasz-tételt, és használjuk föl a feltételeket: | |
Ezek az összefüggések természetesen elfajuló és háromszögekre is teljesülnek. Adjuk össze a kapott egyenlőtlenségeket: amiből következik: . Ez pontosan akkor lehetséges, ha , és így , továbbá és . Ezért a feltételeket figyelembe véve és , amiből . A háromszög tehát derékszögű és egyenlő szárú, ezért a szögei: , , .
| Breuer János (Budapest, ELTE Apáczai Csere J. Gimn., 9. o.t.) |
|
|
 PDF |
PDF |  MathML
MathML