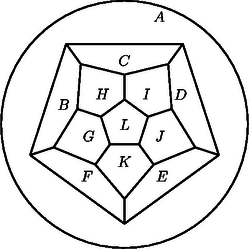
A dodekaéder 12 lapja közül mindegyik pontosan 5 másikkal szomszédos. A lapokat $A$-tól $L$-ig megbetűzzük úgy, hogy a dodekaéder két lapja pontosan akkor legyen szomszédos, amikor az 1. ábrán a megfelelő betűvel jelölt tartományok szomszédosak (az 1. ábrát úgy kaphatjuk, hogy a dodekaédert egy, az $A$ jelű lap ,,fölött'' lévő pontból az $L$ jelű lap síkjára vetítjük.)
Tegyük fel, hogy $A$ piros. Ekkor $B$, $C$, $D$, $E$ és $F$ nem piros. Ha $L$ piros, akkor $G$, $H$, $I$, $J$ és $K$ nem lehet piros, ha pedig $L$ nem piros, akkor $G$, $H$, $I$, $J$ és $K$ közül legfeljebb kettő lehet piros. Azaz az $A$-val megegyező színű lapokból ‐ $A$-t is beleszámítva ‐ legfeljebb három van. A dodekaéder szimmetriái miatt ezt nyilván minden lapjáról elmondhatjuk. Vagyis mind a négy szín legfeljebb három lapon fordul elő; viszont összesen 12 lapunk van, ezért mind a négy színnel pontosan három lap van befestve.
Írjuk minden csúcshoz oda azt a három színt, amilyen színű lapok a csúcsban találkozhatnak. Mivel azonos színű lapoknak nincs közös csúcsuk, és minden színű lapból három van, azért minden színt összesen $5\cdot 3=15$ csúcshoz írtuk oda, és így $20-15=5$ csúcshoz nem írtunk színt. Kék és zöld lapot összekötő él nyilván minden olyan csúcsból pontosan egy indul, ahol vagy a piros vagy a sárga szín nem szerepel. Ez összesen $2\cdot 5=10$ csúcs, de mivel minden élnek két vége van, azért összesen 5 olyan él van, amelyhez csatlakozó két lap közül az egyik kék, a másik pedig zöld.