Kezdőlap


Feladat:	F.3229	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Csendes Viktor
Füzet:	1998/október, 421. oldal		PDF \| MathML
Témakör(ök):	Hozzáírt körök, Háromszögek geometriája, Mértani közép, Feladat
Hivatkozás(ok):	Feladatok: 1998/április: F.3229

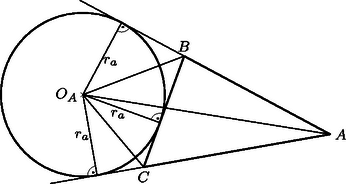
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a háromszög csúcsait a szokásos módon $A$ , $B$ , $C$ -vel, a hozzáírt körök sugarait $r_{a}$ , $r_{b}$ , $r_{c}$ -vel, az $a$ oldalhoz hozzáírt kör középpontját pedig $O_{A}$ -val.
Az $A B C$ háromszög területét megkapjuk, ha az $O_{A} A B$ és az $O_{A} A C$ háromszögek területének összegéből levonjuk az $O_{A} B C$ háromszög területét. E háromszögek mindegyikében az $O_{A}$ -hoz tartozó magasság $r_{a}$ , tehát

\begin{matrix} T_{A B C} = \frac{r_{a} c}{2} + \frac{r_{a} b}{2} - \frac{r_{a} a}{2} . \end{matrix}

(1)

Ugyanígy kapjuk, hogy

\begin{matrix} \begin{matrix} T_{A B C} & = \frac{r_{b} c}{2} + \frac{r_{b} a}{2} - \frac{r_{b} b}{2} és & (2) \\ T_{A B C} & = \frac{r_{c} a}{2} + \frac{r_{c} b}{2} - \frac{r_{c} c}{2} . & (3) \end{matrix} \end{matrix}

Az (1) és (2) egyenletek jobb oldalának szorzata megegyezik a (3) egyenlet jobb oldalának négyzetével, azaz

\begin{matrix} [\frac{r_{a}}{2} (c + b - a)] [\frac{r_{b}}{2} (c + a - b)] = {[\frac{r_{c}}{2} (a + b - c)]}^{2} . \end{matrix}

Felhasználva, hogy

r_{a}

és

r_{b}

mértani közepe

r_{c}

, vagyis

r_{a} r_{b} = r_{c}^{2}

\begin{matrix} (c + b - a) (c + a - b) = {(a + b - c)}^{2} . \end{matrix}

Ebből adódik a feladat megoldása:

c = \frac{a^{2} + b^{2}}{a + b}

Csendes Viktor (Kaposvár, Táncsics M. Gimn., 11. o.t.) dolgozata alapján