Feladat:	Gy.3181	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Papp Dávid
Füzet:	1998/október, 406 - 407. oldal		PDF  |  MathML
Témakör(ök):	Négyszög alapú gúlák, Köréírt gömb, Beírt gömb, Háromszögek hasonlósága, Koszinusztétel alkalmazása, Gyakorlat
Hivatkozás(ok):	Feladatok: 1998/január: Gy.3181

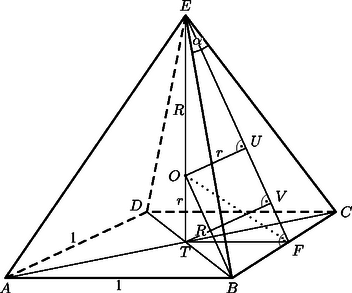
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Az ábrán $O$ a körülírt és a beírt gömb közös középpontja, $R$, illetve $r$ a sugarak, és $AB=1$. Az $E$ csúcs alapsíkra való vetülete $T$, $F$ a $BC$ felezőpontja, $U$ a beírt gömbnek az $ABC$ oldalon vett érintési pontja. Az $OTF$ és $OUF$ derékszögű háromszögek egybevágók, mert megegyeznek két oldalban és a nagyobbal szemközti szögben. Ezért $FU=FT=\frac{1}{2}$. Ugyanígy egybevágóak az $OUE$ és $OTB$ háromszögek, amiért $EU=BT=\frac{\sqrt[]{2}}{2}$. Ezért $EF=EU+FU=\frac{1+\sqrt[]{2}}{2}$. Az oldalélek szögének a felére: $\text{<span style="font-weight: normal;font-style: normal;">tg</span>}\frac{\alpha }{2}=\frac{\frac{1}{2}}{\frac{1+\sqrt[]{2}}{2}}=\sqrt[]{2}-1$, amiből táblázattal vagy zsebszámológéppel $\frac{\alpha }{2}=22\mathrm{,}{5}^{\circ }$ és így $\alpha ={45}^{\circ }$. Arra gondolhatunk azonban, hogy a kapott érték nem pontos. Számítsuk ki a pontos $\alpha$ érték megkeresése érdekében a gúla oldalélét: $\begin{array}{c}{\displaystyle BE=\sqrt[]{{\left(\frac{1}{2}\right)}^2+{\left(\frac{1+\sqrt[]{2}}{2}\right)}^2}=\sqrt[]{\frac{2+\sqrt[]{2}}{2}}\mathrm{.}}\end{array}$ Ezután az $EBC$ háromszögből a koszinusztétel szerint: $\begin{array}{c}{\displaystyle \text{cos}\alpha =\frac{2\cdot \frac{2+\sqrt[]{2}}{2}-1}{2\cdot \frac{2+\sqrt[]{2}}{2}}=\frac{1+\sqrt[]{2}}{2+\sqrt[]{2}}=\frac{\sqrt[]{2}}{2}\mathrm{,}}\end{array}$ amiből $\alpha ={45}^{\circ }$.  Papp Dávid (Budapest, Szent István Gimn. 10.o.t.)   II. megoldás. Papp Dávid két megoldást is adott erre a feladatra. Az ábra alapján könnyen követhető számításait vázlatosan közöljük. A párhuzamos szelők tétele szerint $TV=\frac{r\left(R+r\right)}{R}$. A Pitagorasz-tétel alapján: $EF=\sqrt[]{{\left(R+r\right)}^2+\frac{1}{4}}$. Fejezzük ki ezután kétféleképpen az $ETF$ háromszög kétszeres területének négyzetét: $\begin{array}{c}{\displaystyle \frac{r^2{\left(R+r\right)}^2}{R^2}\cdot \left[{\left(R+r\right)}^2+\frac{1}{4}\right]=\frac{{\left(R+r\right)}^2}{4}\mathrm{.}}\end{array}$ (1) A $BOT$ háromszögből: $\begin{array}{c}{\displaystyle R^2=r^2+\frac{1}{2}\mathrm{.}}\end{array}$ (2) Az $\left(1\right)$ és $\left(2\right)$ egyenletekből álló egyenletrendszerből $r=\frac{\sqrt[]{\sqrt[]{2}-1}}{2}$, amivel $\begin{array}{c}{\displaystyle BE=\sqrt[]{{\left(R+r\right)}^2+\frac{1}{2}}=\sqrt[]{{\left(\sqrt[]{r^2+\frac{1}{2}}+r\right)}^2+\frac{1}{2}}=\sqrt[]{\frac{2+\sqrt[]{2}}{2}}\mathrm{.}}\end{array}$ Végül ugyanúgy, mint az első megoldásban, $\alpha ={45}^{\circ }$.