Feladat: 1997. évi Kürschák matematikaverseny 3. feladata Korcsoport: 18- Nehézségi fok: nehéz
Füzet: 1998/február, 70 - 72. oldal  PDF  |  MathML 
Témakör(ök): Gráfelmélet, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):Feladatok: 1998/február: 1997. évi Kürschák matematikaverseny 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A feladat állítását hurokél és többszörös él nélküli gráfokra, ún. egyszerű gráfokra bizonyítjuk. (Hurokél minden színezésnél egyszínű körhöz vezetne, és egy négy éllel összekötött pontpár esetén már szintén keletkeznék kör.)
Szükségünk lesz a síkra rajzolható gráfok két ismert tulajdonságára (ezek bizonyításával kapcsolatban lásd megjegyzéseinket):

*1) Síkra rajzolható gráfban nem lehet teljes ötszög, azaz öt olyan pont, amelyek közül bármely kettőt él köt össze.
*2) Tetszőleges síkra rajzolható gráf tartalmaz legfeljebb 5-ödfokú pontot, azaz olyan pontot, amelyből legfeljebb 5 él indul ki.
Az állítást a pontok száma szerinti indukcióval bizonyítjuk. 1, 2 és 3 pontú gráfokra az állítás triviális. Tegyük fel, hogy az állítás igaz n csúcsú gráfokra, és tekintsünk egy tetszőleges n+1 csúcsú síkra rajzolható gráfot. Ennek létezik legfeljebb 5-ödfokú pontja, legyen P egy ilyen pont. A P pont foka szerint három esetet különböztetünk meg.

I. eset: P legfeljebb 3-adfokú. Hagyjuk el P-t a belőle induló élekkel együtt. A megmaradó G' gráf továbbra is síkra rajzolható, és az indukciós feltétel szerint jól színezhető, azaz nem lesz benne egyszínű kör. Ezután G' egy jó színezéséhez a P-ből induló éleket színezzük különbözőre. Egyszínű kör G'-ben nincs, és a P-n átmenő körök is tartalmaznak két P-ből induló, különböző színű élt, a kapott színezés tehát jó.
II. eset: P 4-edfokú. Legyenek a P-vel összekötött pontok A, B, C és D. Ezek között van kettő ‐ mondjuk A és B ‐, amelyek között nincs él, mert P-vel együtt nem alkothatnak teljes ötszöget. Hagyjuk el a P pontot a belőle kiinduló élekkel együtt, és húzzuk be az AB élt (Ez lehetséges, pl. az eredeti AP, PB élekhez elég közel, ld. 8. ábra). A keletkező G' gráfot színezzük jól. Tegyük fel, hogy az AB él az 1-es színt kapta. Ezután színezzük G-ben az AP, PB éleket az 1-es színnel, PC-t és PD-t pedig a 2-es és a 3-as színnel. A G' jó színezése miatt egyszínű kör csak P-n keresztül haladhatna, és csak a P-ből kiinduló két egyszínű élen, AP-n és PB-n keresztül. Akkor azonban G' is tartalmazna 1-es színű kört az AB élen keresztül.
III. eset: P ötödfokú. Legyenek a P-ből kiinduló élek a körüljárás sorrendjében PA, PB, PC, PD és PE. Ha az AB, BC, CD, DE és EA élek valamelyike nem szerepelne G-ben, akkor húzzuk be. (Ez lehetséges, mert például ha AB nem szerepel, akkor az A és B pontokat összeköthetjük az AP és PB élekhez elég közel.) Ha ezt a bővített gráfot jól színezzük, az az eredeti gráfnak is egy jó színezését adja. A továbbiakban feltehetjük tehát, hogy az AB, BC, CD, DE és EA élek szerepelnek a gráfban.
Ezután megmutatjuk, hogy a P és a belőle induló élek elhagyása után az ABCDE ötszögnek meghúzható két, egy csúcsból induló átlója. Ha egyik átló sem szerepel G-ben, akkor behúzhatjuk AC-t és AD-t az AP és PC, illetve AP és PD élekhez elég közel. Az új élek csak a PB és PE élt metszik, így a keletkező G' gráf síkra rajzolható. Ha például a BE él szerepel G-ben, akkor a BEP háromszög elválasztja A-t C-től és D-től, így G-ben nem szerepelhet sem az AC, sem az AD él. Húzzuk meg ezeket az előbbi módon, majd hagyjuk el P-t a belőle induló élekkel együtt, így most is síkra rajzolható G' gráfot kapunk, mert az új élek csak PB-t és PE-t metszik. Az indukciós feltevés szerint G' jól színezhető (9. ábra).
Színezzük jól a G' gráfot. Ha a színezésben AC és AD ugyanolyan, mondjuk 1-es színű, akkor G-nek a G'-ben is szereplő élei színét megtartva színezzük az AP, CP és DP éleket 1-es színnel, a BP és EP éleket 2-es, illetve 3-as színnel (10. ábra). Ha az így kapott gráfban van egyszínű kör, akkor az ismét csak 1-es színű lehet, P-n keresztül halad az AP és PC, az AP és PD vagy pedig a CP és PD éleken keresztül. Ezekben az esetekben viszont G' is tartalmaz egyszínű kört az AC, az AD, illetve a CA és AD éleken keresztül. A továbbiakban ezért feltesszük, hogy AC és AD színe különböző: 1-es, illetve 2-es.
Hagyjuk el az AC és AD átlókat, és vizsgáljuk meg, hogy az ötszög csúcspárjai milyen színű utakkal köthetők össze. Ha létezik két olyan csúcspár: X, Y és U, V, amelyek közül X és Y nem köthető össze 1-es, U és V pár pedig nem köthető össze 2-es színnel, akkor színezzük ki PX-et és PY-t 1-es színnel, PU-t és PV-t 2-es színnel, a P-ből kiinduló ötödik élt pedig 3-as színnel (11. ábra). Ezzel a G gráf egy jó színezését kapjuk.
Mivel az AC él 1-es színű volt, A és C nem köthető össze 1-es színnel; hasonlóképpen A és D nem köthető össze 2-es színnel. Ha a B, D, E csúcsok közül valamelyik kettő nem köthető össze 2-es színnel, akkor azt a kettőt U, V-nek, A, C-t pedig X, Y-nak választva, az előbbiek szerint G-nek egy jó színezését nyerjük. Ha viszont B, D és E összeköthető 2-es színnel, akkor A nem köthető össze B-vel és E-vel 2-es színű úton, mert akkor A és D is összeköthető lenne 2-es színnel. Hasonlóképpen feltehetjük, hogy a B, C és E csúcsok összeköthetők 1-es színnel, míg az A csúcs nem köthető össze a B és E csúcsokkal 1-es színű úton sem (12. ábra).
Az A csúcs tehát nem köthető össze a B, és E csúcsokkal sem 1-es, sem 2-es színű úton. Ebből következik, hogy az AB és AE élek színe 3-as, és az A, B, E csúcsok között csak ezek az élek alkotnak 3-as színű utat. Színezzük át AB-t 1-esre, AE-t pedig 2-esre. Ezzel a változtatással nem keletkezhet egyszínű kör. Ezután színezzük ki a PA, PB és PE éleket 3-asra, a PC és PD eleket pedig 1-esre, illetve 2-esre (13. ábra). Ha lenne egyszínű kör, akkor az csak P-n keresztül haladhatna, és csak 3-as színű lehetne, és azt jelentené, hogy az A, B és E csúcsok közül valamelyik kettő között még egy 3-as színű út halad, ami ellentmondás.
Ezzel minden n+1 csúcsú gráfra igazoltuk az állítást.
 

Megjegyzések. 1. Az, hogy a teljes ötszög nem síkra rajzolható, például a következőképpen mutatható meg: Kössük össze a pontokat valamilyen sorrendben egymást nem metsző élekkel. A keletkező ötszög belsejében is, rajta kívül is csak két-két pontpárt köthet össze él, ezek a megmaradó csúcspárt elválasztják egymástól (14. ábra).
2. Síkra rajzolható gráfok a síkot lapokra bontják, ezekhez hozzávéve a gráfon kívüli tartomát is. Ha a gráf összefüggő, akkor a lapok l, az élek é és a csúcsok c száma között fennáll az Euler-féle l-é+c=2 összefüggés. Ha a csúcsok száma legalább 3, akkor egy lapnak legalább 3 oldala van, másrészt minden él két lapnak oldala, így 3l≤2é. Ezt az Euler-tételbe helyettesítve az é≤3c-6 egyenlőtlenség adódik. Ha minden csúcs legalább 6-odfokú lenne, akkor ‐ mivel minden él két csúcshoz tartozik ‐, é≥c teljesülne.
3. Könnyen igazolható, hogy ha egy k csúcsú gráf nem tartalmaz kört, akkor legfeljebb k-1 éle van. Ha azt vizsgáljuk, hogy egy tetszőleges G gráf élei mikor színezhetők ki 3 színnel úgy, hogy ne legyen benne egyszínű kör, akkor szükséges, hogy tetszőleges k pozitív egészre G bármely k csúcsa között legfeljebb 3k-3 él haladjon. Ez a feltétel gyengébb, mint a síkra rajzolhatóság, és be lehet bizonyítani, hogy nemcsak szükséges, hanem elégséges is.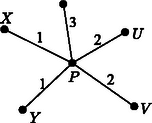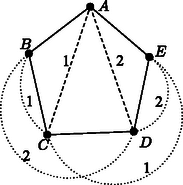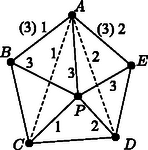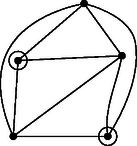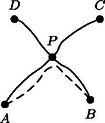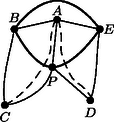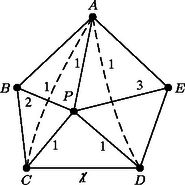