Kezdőlap


Feladat:	1997. évi Kürschák matematikaverseny 2. feladata	Korcsoport: 16-17	Nehézségi fok: nehéz
Füzet:	1998/február, 67 - 70. oldal		PDF \| MathML
Témakör(ök):	Feuerbach-kör, Magasságpont, Beírt kör, Körülírt kör, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):	Feladatok: 1998/február: 1997. évi Kürschák matematikaverseny 2. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Tekintsük az

O

O_{1}

és

M_{1}

pontok merőleges vetületeit az

A_{1} B_{1} C_{1}

háromszög oldalaira. Elegendő azt megmutatni, hogy az ezek közti szakaszok aránya két különböző oldalon megegyező. Határozzuk meg ezt az arányt pl. a

B_{1} C_{1}

oldalon.

F

-fel jelölve az

A B C

háromszög köré írt kör

A

-t nem tartalmazó

B C

ívének felezőpontját, ezen átmegy az

O

-ból a

B C

oldalra emelt merőleges is és az

A

-ból induló szögfelező is. Jelöljük a köztük levő szöget

δ

-val (2. ábra). Az

O_{1} A_{1}

érintési sugár szintén merőleges a

B C

oldalra.

O

O_{1}

és

M_{1}

merőleges vetületét a

B_{1} C_{1}

oldalon jelöljük

O'

O_{1}'

és

M_{1}'

-vel. Az

A B_{1} C_{1}

háromszög egyenlő szárú, ezért

O_{1}'

A F

-en van, tehát

A_{1} M_{1}

párhuzamos

A F

-fel, és így

O_{1} A_{1} M_{1} ∢ = δ

. Az

O

-ból

A F

-re és

O_{1}

-ből

A_{1} M_{1}'

-re emelt merőleges szakaszok egyrészt az

O' O_{1}'

, illetőleg

O_{1}' M_{1}'

szakasszal egyenlők, másrészt hosszuk

R sin δ

, illetőleg

r sin δ

, ahol

R

a háromszög köré írt kör sugara,

r

a beírt köré. Így

\begin{matrix} O' O_{1}' : O_{1}' M_{1}' = (R sin δ) : (r sin δ) = R : r . \end{matrix}

Ez az arány azonban csak a két kör adataitól függ, a

B_{1} C_{1}

oldaltól nem, így ugyanez az arány adódik a másik két oldalon levő vetületek közti szakaszokra is. Ezzel a feladat állítása bizonyítást nyert.

II. megoldás. A megoldáshoz felhasználunk a háromszögekre vonatkozó néhány összefüggést, amelyeket a megoldás végén bizonyítunk.
Jelöljük az

A_{1} B_{1} C_{1}

háromszög csúcsaiból húzott magasságok talppontját rendre

A_{2}

B_{2}

C_{2}

-vel (3. ábra).
a) Egy háromszög magasságai felezik a talpponti háromszög szögeit, így a magasságpont a talpponti háromszögbe írt kör középpontja, esetünkben

M_{1}

A_{2} B_{2} C_{2}

-be írté.
b) Ismeretes, hogy a háromszög (esetünkben az

A_{1} B_{1} C_{1}

háromszög) köré írt körnek a csúcsokhoz mutató sugarai merőlegesek a talpponti háromszög oldalaira. Esetünkben

O_{1} A_{1}

O_{1} B_{1}

O_{1} C_{1}

érintési sugár is, tehát merőleges rendre a

B C

C A

A B

oldalra is, tehát az

A B C

és az

A_{2} B_{2} C_{2}

háromszög oldalai párhuzamosak.
c) A két háromszög hasonló helyzetű is, s így rájuk vonatkozóan megfelelő pontpárok összekötő egyenesei is párhuzamosak.
d) Az

A_{2} B_{2} C_{2}

háromszög köré írt kör az

A_{1} B_{1} C_{1}

háromszög ún. Feuerbach-köre, ez átmegy az oldalak felezőpontjain is, és középpontja az

O_{1} M_{1}

szakasz

F_{0}

felezőpontja.
Az

A B C

háromszögre vonatkozóan

O

és

O_{1}

megfelelői az

A_{2} B_{2} C_{2}

-re vonatkozóan

F_{0}

és

M_{1}

, így összekötő egyeneseik párhuzamosak. A két egyenesnek azonban

O_{1}

közös pontja, így

O

O_{1}

és

M_{1}

egy egyenesen van, és ezt kellett bizonyítani.

Bebizonyítjuk a felhasznált összefüggéseket.
a) Jelöljük az

A B C

háromszög egymás utáni csúcsaiból húzott magasságainak talppontját

T_{a}

T_{b}

T_{c}

-vel (4. ábra). Az

A B T_{a} T_{b}

és az

A C T_{a} T_{c}

négyszög húrnégyszög, így

T_{c} T_{a} B ∢ = C A B ∢

és

T_{b} T_{a} C ∢ = B A C ∢

, tehát

A T_{a}

szögfelező.
b) Az

A B C

háromszög köré írt

O

középpontú körben az

A O B ∢

mint középponti szög az

A C B ∢

kétszerese (5. ábra). Szögfelezője merőleges

A B

-re, és

A C B ∢

nagyságú szöget zár be vele. A

C

pontból húzott magasság

T_{c}

talppontjából állítsunk merőlegest

O A

-ra, messe ez a

C A

oldal egyenesét a

T^{*}

pontban. Ekkor

A T_{c} T^{*} ∢

mint merőleges szárú szög ugyancsak

A C B ∢

nagyságú, tehát

B C T^{*} T_{C}

húrnégyszög, benne a

B C

oldal

T_{C}

-ből derékszögben látszik, tehát

T^{*}

-ból is, vagyis

T^{*}

B

-ből húzott magasság talppontja,

T_{b}

.
c) Azt kell belátnunk, hogy ha az

A B C

és az

A_{2} B_{2} C_{2}

háromszög megfelelő oldalai párhuzamosak, akkor

A A_{2}

B B_{2}

és

C C_{2}

egy ponton megy keresztül, vagy párhuzamosak (6. ábra). Ha pl.

A A_{2}

és

B B_{2}

metszi egymást egy

T

pontban, akkor

A B T

és

A_{2} B_{2} T

hasonló háromszögek, így

A T : A_{2} T = A B : A_{2} B_{2} = B T : B_{2} T

. Másrészt

A B : A_{2} B_{2} = B C = B_{2} C_{2}

. Ekkor azonban a

B C T

és a

B_{2} C_{2} T

háromszög is hasonló, mert egy szögük és az azt közrefogó oldalak aránya egyenlő. Ebből viszont következik, hogy

C

C_{2}

és

T

is egy egyenesen van.
d) A Feuerbach-körre vonatkozó állítások igazolására jelöljük a

B C

C A

A B

oldalak felezőpontjait rendre

F_{a}

F_{b}

F_{c}

-vel (7. ábra. Az

A

csúcs tükörképe az

F_{b} F_{c}

középvonalra a

T_{a}

magasságtalppont.

F_{a} F_{c}

mint középvonal

F_{b} A

-val egyenlő és párhuzamos, a tükrözés folytán pedig

F_{b} T_{a}

-val egyenlő. Így

F_{a} T_{a} F_{b} F_{c}

szimmetrikus trapéz (lehet hurkolt, esetleg egyenlő szárú háromszög). Így kör írható köré, amelynek középpontja az

F_{a} T_{a}

szakasz felezőmerőlegesén van, az pedig felezi az

O

és az

M

magasságpont közti szakaszt.
A kör átmegy mind a három oldal felezőpontján, így a gondolatot a másik két oldalra megismételve, ugyanaz a kör adódik, sőt, azt is kapjuk, hogy a kör középpontja az

O M

szakasz

F_{0}

felezőpontja. Az oldafelezőpontok és a magasságtalppontok közül bármelyik 3 különböző már meghatározza a kört.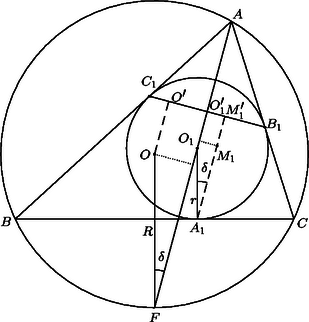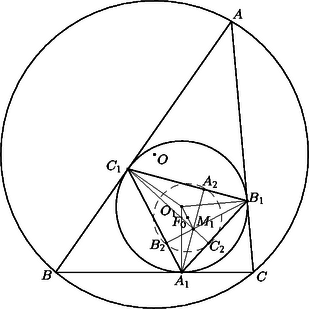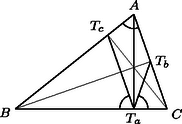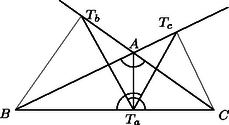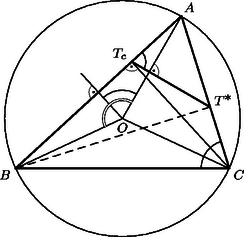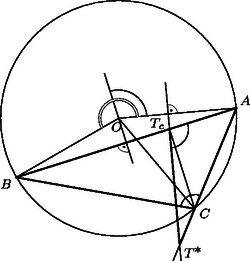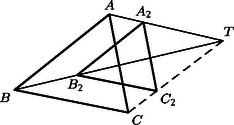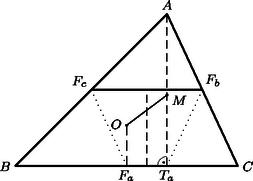