Kezdőlap


Feladat:	1997. évi Kürschák matematikaverseny 1. feladata	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):
Füzet:	1998/február, 66 - 67. oldal		PDF \| MathML
Témakör(ök):	Két pont távolsága, szakasz hosszúsága, Oszthatósági feladatok, Maradékos osztás, Prímszámok, Négyzetrács geometriája, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):	Feladatok: 1998/február: 1997. évi Kürschák matematikaverseny 1. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Bebizonyítjuk, hogy azok az $A : (i, y (i))$ pontok, amelyeknél $y (x)$ az $x^{2}$ (legkisebb nemnegatív) maradéka $p$ -vel történő osztásnál ( $0 \leq i \leq p - 1$ ), kielégítik a követelményt. Az értelmezés szerint $y (x) = x^{2} + c p$ alkalmas $c$ egésszel.
Tegyük fel, hogy az $A_{i} A_{j}$ és az $A_{i} A_{k}$ szakaszok meredeksége egyenlő volna:

\begin{matrix} \frac{y (j) - y (i)}{j - i} = \frac{y (k) - y (i)}{k - i} . \end{matrix}

A törteket eltávolítva, az értelmezést felhasználva és átrendezve:

\begin{matrix} (k - i) (j^{2} - i^{2} + (v - u) p) = (j - i) (k^{2} - i^{2} + (w - u) p), \end{matrix}

továbbrendezve és alakítva

\begin{matrix} (k - i) (j - i) (j - k) = p ((j - i) (w - u) - (k - i) (v - u)) . \end{matrix}

A bal oldali szorzatnak kellene tehát oszthatónak lennie

p

-vel. Ez azonban nem lehetséges, mert egy szorzat csak úgy lehet osztható egy prímszámmal, ha valamelyik tényezője osztható vele, itt pedig mindegyik tényező 0-tól különböző és abszolút értékük

p

-nél kisebb. Nem lehet tehát a két meredekség egyenlő.

Megjegyzések. 1. Az

x^{2}

helyett bármilyen egész együtthatós vagy egész helyeken egész értéket felvevő, másodfokú polinom megfelel. Érdekes, hogy a feladattal foglalkozó versenyzők többnyire az

\frac{x (x + 1)}{2}

polinomot választották.
2. Többen használtak olyan pontatlan állításokat, mint különbség maradéka egyenlő a maradékok különbségével, vagy szorzat maradéka egyenlő a tényezők maradékainak szorzatával, amelyek csak kiegészítésekkel érvényesek.
3. Egy versenyző azokat az

(x, y)

pontokat adta meg, amelyekre

x y \equiv 1

(mod

p

) (

1 \leq x \leq p - 1

), maga is megjegyezve, hogy így csak

p - 1

pontot kap.
4. A kérdésnek kiterjedt irodalma van. A feladat állítása igaznak látszik prímszám helyett minden pozitív egész számra, sőt próbálgatások során

n = 32

-ig és számos nagyobb páros

n

-re

2 n

pontot is sikerült találni úgy, hogy ne legyen közülük 3 egy egyenesen. Sikerült bebizonyítani, hogy tetszés szerinti pozitív

h

értékhez

(3 / 2) - h) n

pont is kiválasztható, ha

n

elég nagy.
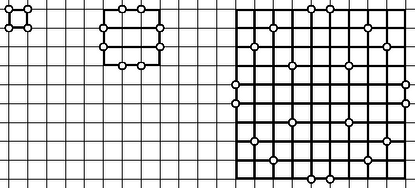
A problémával kapcsolatban R. K. Guy és P. A. Kelly több érdekes sejtést fogalmazott meg. Így többek közt azt sejtik, hogy csak az 1. ábrán látható 3 esetben helyezhető el

2 n

pont egy

n

oldalhosszú négyzetben úgy, hogy rendelkezzék a négyzet összes szimmetriájával; azt sejtik továbbá, hogy nagy

n

-re legfeljebb

(c + h) n

pont helyezhető el a követelménynek megfelelően, ahol

c = {(2 π^{2} / 3)}^{1 / 3} \approx 1, 85

. ^{$^{*}$}R. K. Guy: Unsolved problems in number theory, 2. kiad. Springer, 1996. XVI + 285 old., közelebbről 242‐244. old.

^{$^{*}$}

^{1}