Feladat:	Gy.3162	Korcsoport: 16-17	Nehézségi fok: könnyű
Megoldó(k):	Börzsönyi Ádám ,  Harangi Viktor ,  Máthé András ,  Rischák Rózsa ,  Tóth Ágnes ,  Varga Szilvia
Füzet:	1998/május, 283 - 284. oldal		PDF  |  MathML
Témakör(ök):	Derékszögű háromszögek geometriája, Beírt kör, Pitagorasz-tétel alkalmazásai, Gyakorlat
Hivatkozás(ok):	Feladatok: 1997/november: Gy.3162

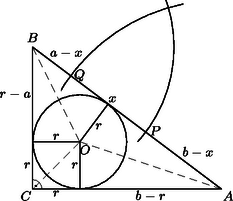
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Az $a$, illetve $b$ sugarú kör az átfogót a $P$ és $Q$ pontokban metszi (lásd az ábrát). Az $x=PQ$ jelöléssel $a-x+x+b-x=c$, amiből $\begin{array}{c}{\displaystyle x=a+b-c\mathrm{.}}\end{array}$ (1) A beírt körhöz az $A$ és $B$ pontokból húzott érintőszakaszok $a-r$ és $b-r$, ezért $a-r+b-r=c$, rendezve az egyenletet $\begin{array}{c}{\displaystyle 2r=a+b-c\mathrm{.}}\end{array}$ (2) (1) és (2)-ből következik a feladat állítása.  Rischák Rózsa (Hódmezővásárhely, Kertvárosi Ált. Isk., 8. o.t.)   Megjegyzés. A bizonyítás szempontjából teljesen mindegy, hogy melyik végpontból rajzoltuk meg az $a$, illetve $b$ sugarú kört, azok helyzetére vonatkozóan semmit nem használtunk fel. A bizonyítás során csak $b-x$, illetve $a-x$ helyzete cserélődik fel.   II. megoldás. Az ábrán a $PB=a$ és $QA=b$ szakaszok úgy fedik le a $c$ átfogót, hogy a $PQ$ szakasz kétszeresen van lefedve, ezért $c=a+b-x$, így $x=a+b-c$. Az $ABC$ derékszögű háromszög $\frac{a\cdot b}{2}$ területe három $O$ csúcsú háromszög területének összege, így $\begin{array}{c}{\displaystyle \frac{a\cdot b}{2}=\frac{a\cdot r}{2}+\frac{b\cdot r}{2}+\frac{c\cdot r}{2}\mathrm{,}}\end{array}$ amiből $2r=\frac{2ab}{a+b+c}$. A feladat állításához azt kell bizonyítanunk, hogy $x=2r$, azaz $a+b-c=\frac{2ab}{a+b+c}$. Rendezve: azzal, hogy ${\left(a+b\right)}^2-c^2=2ab$, ahonnan $a^2+b^2=c^2$. Ez a Pitagorasz-tétel alapján igaz, amiből visszafelé következtetve a feladat állítását kapjuk.  Börzsönyi Ádám (Hódmezővásárhely, Bethlen G. Ref. Gimn., 9. évf.) és    Harangi Viktor (Fazekas M. Főv. Gyak. Gimn., 8. o.t.)