Kezdőlap


Feladat:	C.483	Korcsoport: 16-17	Nehézségi fok: könnyű
Megoldó(k):	Ábrány Miklós , Andrássy Zoltán , Antal István , Bákor Krisztina , Benke Noémi , Biczó Mihály , Csató György , Csizmadia Zsolt , Csóka Endre , Csordás Hunor , Csökmei Krisztina , Dőry Magdolna , Gueth Krisztián , Horváth Illés , Németh Ádám , Pozsonyi Tamás , Sarlós Ferenc , Szűcs Zsófia , Tamás Gábor Zoltán , Zeke András
Füzet:	1998/április, 220 - 221. oldal		PDF \| MathML
Témakör(ök):	Deltoidok, Derékszögű háromszögek geometriája, C gyakorlat
Hivatkozás(ok):	Feladatok: 1997/november: C.483

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A feltétel, azaz hogy a négyszög (konvex) deltoid legyen, nyilván elegendő, de nem szükséges. Tekintsük az $A B C D$ deltoidot (1. ábra). Tudjuk, hogy az átlói merőlegesek egymásra, 4 derékszögű háromszögre osztják a deltoidot. A háromszögek területeinek összege egyenlő a deltoid területével. Jelöljük az átlók metszéspontját $O$ -val, az $A O = e_{1}$ , $O C = e_{2}$ , $D O = f_{1}$ , $B O = f_{2}$ jelöléssel

\begin{matrix} T = \frac{f_{1} e_{1}}{2} + \frac{f_{2} e_{1}}{2} + \frac{f_{1} e_{2}}{2} + \frac{f_{2} e_{2}}{2} = \frac{(f_{1} + f_{2}) (e_{1} + e_{2})}{2} = \frac{e f}{2} . \end{matrix}

Az előző számítást azonban bármely olyan konvex négyszögre is alkalmazhatjuk, amelynek átlói merőlegesek egymásra, hiszen sehol sem használtuk fel, hogy a négyszög két-két oldalpárjának hossza megegyezik.
Így tehát ezekre a konvex négyszögekre (nem deltoidokra) is igaz, hogy területük egyenlő az átlók szorzatának felével (2. ábra).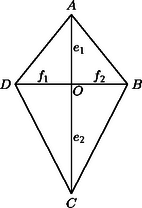

Megjegyzés. Mivel a négyzet és rombusz speciális deltoidok, azokra is igaz az állítás. Ez azonban nem elegendő válasz. Azt kellett belátnunk, hogy létezik olyan négyszög, amely nem deltoid (tehát nem is négyzet vagy rombusz), amelynek a területe a feladatban leírt módon kapható.