Kezdőlap


Feladat:	Gy.3154	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Deli Lajos
Füzet:	1998/október, 405. oldal		PDF \| MathML
Témakör(ök):	Háromszögek nevezetes tételei, Beírt kör, Gyakorlat
Hivatkozás(ok):	Feladatok: 1997/október: Gy.3154

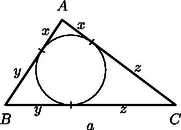
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelölésünk szerint $a = y + z$ , $b = x + z$ , $c = x + y$ ; és mivel $a \geq b \geq c$ , azért $z \geq y \geq x$ . A bizonyítandó egyenlőtlenségekbe $a$ , $b$ és $c$ helyére $y + z$ -t, $x + z$ -t és $x + y$ -t helyettesítve kapjuk, hogy

\begin{matrix} (y + z) z + (x + z) y + (x + y) x \geq \frac{{(y + z)}^{2} + {(x + z)}^{2} + {(x + y)}^{2}}{2} \geq (y + z) x + (x + z) y + (x + y) z . \end{matrix}

Elvégezve a szorzásokat és

(y z + x z + x y)

-t levonva kapjuk, hogy

\begin{matrix} x^{2} + z^{2} + x y + y z - x z \geq x^{2} + y^{2} + z^{2} \geq x y + y z + z x . \end{matrix}

A jobb oldali egyenlőtlenség ismert, közvetlenül adódik a nyilvánvaló

{(x - y)}^{2} + {(y - z)}^{2} + {(z - x)}^{2} \geq 0

egyenlőtlenség átrendezéséből. A bal oldali egyenlőtlenséget átrendezve:

\begin{matrix} x y + y z - x z - y^{2} \geq 0, azaz (z - y) (y - x) \geq 0. \end{matrix}

Esetünkben ez is teljesül, mert

z - y \geq 0

és

y - x \geq 0

feltételünk szerint. Mivel ekvivalens átalakításokat végeztünk, ezzel az eredeti egyenlőtlenséget is beláttuk.
Az is látszik, hogy a jobb oldali egyenlőtlenségben csak szabályos háromszög esetén van egyenlőség, míg a bal oldaliban

y = x

vagy

z = y

esetén, azaz ha a háromszög

b

oldala valamelyik másikkal egyenlő.

Deli Lajos (Hajdúszoboszló, Hőgyes E. Gimn., 9. o.t.) dolgozata alapján