Kezdőlap


Feladat:	Gy.3153	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Kunszenti-Kovács Dávid
Füzet:	1998/május, 280. oldal		PDF \| MathML
Témakör(ök):	Szélsőérték-feladatok differenciálszámítás nélkül, Pitagorasz-tétel alkalmazásai, Háromszög-egyenlőtlenség alkalmazásai, Gyakorlat
Hivatkozás(ok):	Feladatok: 1997/október: Gy.3153

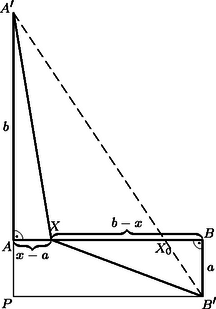
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az általánosság megszorítása nélkül feltehető, hogy $b \geq a$ . Mérjük fel a számegyenesre az $O$ kezdőponttól jobbra az $A$ , $B$ és $X$ pontokat úgy, hogy ezeknek az $O$ -tól mért távolsága rendre $a$ , $b$ és $x$ legyen. (Negatív $x$ esetén az $X$ az $O$ -tól balra volna; ábránkon az $a < x < b$ eset szerepel.) Vegyük fel az $A'$ és $B'$ pontokat az $A B$ egyenes különböző oldalain úgy, hogy $A A'$ is és $B B'$ is merőleges legyen $A B$ -re, továbbá az $\bar{A A'}$ távolság $b$ , a $\bar{B B'}$ távolság $a$ legyen. Ekkor az ábra jelöléseit használva $\bar{A' X} = \sqrt[]{{(x - a)}^{2} + b^{2}}$ és $\bar{X B'} = \sqrt[]{{(x - b)}^{2} + a^{2}}$ ; azaz $K = \bar{A' X} + \bar{X B'}$ .
$P$ a $B'$ ponton át az $A B$ -vel húzott párhuzamos és az $A A'$ metszéspontja. Az $A' B'$ egyenes az $A B$ -t messe az $X_{0}$ pontban. Ekkor a háromszög-egyenlőtlenség alapján:

\begin{matrix} K = \bar{A' X} + \bar{X B'} \geq \bar{A' B'} = \sqrt[]{{\bar{A' P}}^{2} + {\bar{P B'}}^{2}} = \sqrt[]{{(a + b)}^{2} + {(b - a)}^{2}} = \sqrt[]{2 a^{2} + 2 b^{2}} . \end{matrix}

K

-nak a minimuma tehát

\sqrt[]{2 a^{2} + 2 b^{2}}

. Ezt az értéket valóban fel is veszi az

X_{0}

pontban. Ez az

x_{0}

érték az

X_{0}

pontnak a kezdőponttól mért távolsága. Az

A' A X_{0}

és

B B' X_{0}

háromszögek hasonlósága alapján:

\begin{matrix} \frac{x_{0} - a}{b} = \frac{b - x_{0}}{a}, ahonnan x_{0} = \frac{a^{2} + b^{2}}{a + b} adódik. \end{matrix}