Feladat: Gy.3150 Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Babos Attila ,  Béky Bence ,  Birkner Tamás ,  Devecsery András ,  Dombi Tímea ,  Gajári Dávid ,  Gerencsér Balázs ,  Gyenes Zoltán ,  Hesz Gábor ,  Hudomiet Péter ,  Kerékfy Péter ,  Keszegh Balázs ,  Kiss Gergely ,  Kunszenti-Kovács Dávid ,  Lengyel Tímea ,  Naszódi Gergely ,  Németh András ,  Pap Júlia ,  Papp Dávid ,  Pataki Péter ,  Szécsi Vajk ,  Székelyhidi Gábor ,  Terpai Tamás ,  Tillinkó Zsanett ,  Végh A. László ,  Venter György ,  Vizer Máté ,  Zábrádi Gergely 
Füzet: 1998/április, 222 - 223. oldal  PDF  |  MathML 
Témakör(ök): Kombinációk, Halmazelmélet, Gyakorlat
Hivatkozás(ok):Feladatok: 1997/október: Gy.3150

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a megállók számát n-nel. Ekkor a megálló-párok száma (n2). Tudjuk, hogy bármely két megálló között van buszjárat, és hogy bármely két buszjáratnak 1 közös megállója van, tehát 2 megálló között pontosan egy buszjárat közlekedik. Mivel minden buszjáratnak 3 megállója van, ezért a buszjáratok száma 13⋅(n2)=n(n-1)6, így a járatok páronkénti közös megállóinak száma

k=(n(n-1)62)=n(n-1)6(n(n-1)6-1)2.
Másrészt minden megállóban n-12 buszjárat áll meg (minden buszjárathoz 2 másik megálló van), ezért minden megálló ((n-1)22)=n-12⋅(n-12-1)2 közös megállónak felel meg. Tehát k=n⋅n-12(n-12-1)2, vagyis
n(n-1)6⋅(n(n-1)6-1)2=n⋅n-12(n-12-1)2.
Ebből n2-10n+21=0, azaz n=3 vagy n=7.
Az n=3 esetben 1 buszjárat van, amire nyilvánvaló a feladat állítása. Az n=7 esetben 7 buszjárat van, amire a következő példát lehet mutatni:
Ha a buszmegállókat 1, 2, 3, ..., 7-tel jelöljük, akkor a következő buszjáratok kielégítik a feladat feltételeit:
{1,2,3},{1,4,5},{1,6,7},{2,4,6},{2,5,7},{3,4,7},{3,5,6}.
Tehát 1 vagy 7 buszjárat lehet a városban.
 Székelyhidi Gábor (Kuwait, New English School, 11. évf.)

 
Megjegyzés. A feladatbeli megállók járatonkénti csoportosítása speciális esete a következő típusú konfigurációknak. Tekintsünk egy n elemű halmazt és ennek bizonyos részhalmazait azzal a két tulajdonsággal, hogy 
(1) bármely két ilyen (különböző) részhalmaznak pontosan egy közös eleme van; és 
(2) bármely két (különböző) elemet véve a halmazban, pontosan egy olyan kijelölt részhalmaz létezik, amelynek mindketten elemei.
Az (1) és (2) tulajdonságoknak eleget tevő halmazrendszereket ‐ bizonyos, nyilvánvalóan triviális elrendezéstől eltekintve ‐ véges projektív síkoknak nevezzük; a természetes geometriai analógia alapján a halmaz elemeit pontoknak, a kijelölt részhalmazokat egyeneseknek hívjuk. Könnyen belátható, hogy egy projektív sík egyeneseinek a száma ugyanannyi, mint a pontok száma, azaz n. Azt sem nehéz bizonyítani, hogy minden egyenesnek ugyanannyi pontja van ‐ szokás ezt a számot (q+1)-gyel jelölni ‐ és ez a szám megegyezik egy tetszőleges ponton átmenő egyeneseknek a számával. Az is egyszerűen adódik ezután, hogy n=q2+q+1.
Az úgynevezett véges testek felhasználásával konstruálni lehet véges projektív síkot minden olyan esetben, amikor q prímhatvány. Vannak azonban olyan síkok, amelyek ezzel az általános eljárással nem állíthatók elő. Olyan síkot azonban még senki sem talált, amelyben q ne lett volna prímhatvány. Ezzel kapcsolatos a véges matematika egy nevezetes, mindeddig megoldatlan problémája: milyen q értékekre létezik q-adrendű véges projektív sík (lehet-e q más is, mint egy prímszám egész kitevős hatványa)?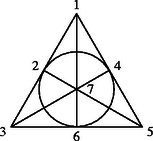