Feladat:	F.3187	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bíró Zsuzsanna ,  Gyenes Zoltán ,  Györkei Györgyi ,  Hegedűs Péter ,  Kunszenti-Kovács Dávid ,  Lengyel Tímea ,  Less Áron ,  Lovas Róbert ,  Stoll Péter ,  Végh A. László
Füzet:	1998/március, 161. oldal		PDF  |  MathML
Témakör(ök):	Körülírt kör, Háromszögek nevezetes tételei, Vektorok, Magasságpont, Derékszögű háromszögek geometriája, Feladat
Hivatkozás(ok):	Feladatok: 1997/szeptember: F.3187

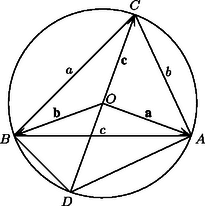
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Bebizonyítjuk, hogy a feladat feltétele pontosan a derékszögű háromszögekre igaz. Legyen először az $ABC$ háromszög hegyesszögű. Az ábrán $O$ a körülírt kör középpontja, $D$ pedig a kör $C$-vel átellenes pontja. Ekkor $8R^2=2{\left(2R\right)}^2=a^2+B{D}^2+b^2+A{D}^2<a^2+b^2+c^2$, hiszen most a $BDA\sphericalangle$ tompaszög, és így $A{D}^2+B{D}^2<c^2$. Ha a háromszög tompaszögű, akkor $2R>c$ miatt $4R^2>c^2$ és $8R^2>2c^2>a^2+b^2+c^2$, ahol $c$ a legnagyobb oldalt jelöli. Derékszögű háromszög esetén $2R=c$, ezért $8R^2=2c^2=a^2+b^2+c^2$, ahol $c$ az átfogó. Tehát $a^2+b^2+c^2=8R^2$ pontosan akkor teljesül, ha a háromszög derékszögű.  Kunszenti-Kovács Dávid (Oslo, Lycée Français René Cassin, 7. o.t.)   II. megoldás. Legyen $O$ a vonatkoztatási pont, és $\overrightarrow{OA}=\text{a}$, $\overrightarrow{OB}=\text{b}$, $\overrightarrow{OC}=\text{c}$. Ekkor $|\text{a}|=|\text{b}|=|\text{c}|=R$, és pl. $|\text{b}-\text{c}|=a$ alapján: $a^2={\left(\text{b}-\text{c}\right)}^2=2R^2-2\text{bc}$, amiből $2\text{bc}=2R^2-a^2$. Hasonlóan kapjuk, hogy $2\text{ab}=2R^2-c^2$, $2\text{ca}=2R^2-b^2$. Legyen $\text{m}$ a magasságpont helyvektora. Ismeretes, hogy $\text{m}=\text{a}+\text{b}+\text{c}$, ezért ${\text{m}}^2={\left(\text{a}+\text{b}+\text{c}\right)}^2=3R^2+6R^2-\left(a^2+b^2+c^2\right)$, amiből $a^2+b^2+c^2=9R^2-\text{m}$. A feladat feltételének azok és csak azok a háromszögek felelnek meg, amelyekre $9R^2-{\text{m}}^2=8R^2$, azaz $R^2={\text{m}}^2$, tehát $|R|=|\text{m}|$. Ez pontosan a derékszögű háromszögekre teljesül.